Finite Impulse Reseponse Decimator (firdecim)

The firdecim object family implements a basic interpolator with an integer output-to-input resampling ratio \(D\) . It is essentially just a firfilt object which operates on a block of samples at a time. An example of the firdecimator can be seen in [ref:fig-filter-firdecim-crcf] .

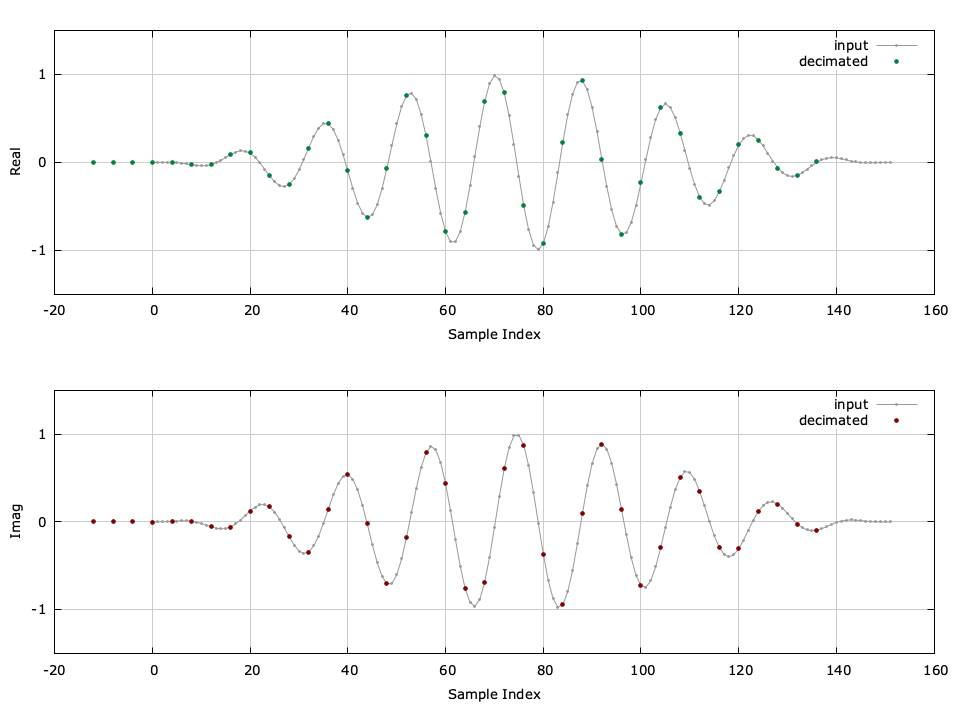
Figure [fig-filter-firdecim-crcf]. firdecim_crcf (firdecimator) example with \(D=4\) , compensating for filter delay.

Listed below is the full interface to the firdecim family of objects. While each method is listed for firdecim_crcf , the same functionality applies to firdecim_rrrf and firdecim_cccf .

• firdecim_crcf_create(D,*h,N) creates a firdecim object with a firdecimation factor \(D\) using \(N\) filter coefficients \(\vec{h}\) .
• firdecim_crcf_create_prototype(D,m,As) creates a firdecim object from a prototype filter with a firdecimation factor \(D\) , a delay of \(Dm\) samples, and a stop-band attenuation \(A_s\) dB.
• firdecim_crcf_create_rnyquist(type,D,m,beta,dt) creates a firdecim object from a square-root Nyquist prototype filter with a firdecimation factor \(D\) , a delay of \(Dm\) samples, an excess bandwidth factor \(\beta\) , and a fractional sample delay \(\Delta t\) (see [ref:section-filter-firdes-rnyquist] for details).
• firdecim_crcf_destroy(q) destroys a firdecim object, freeing all internally-allocated memory.
• firdecim_crcf_print(q) prints the parameters of a firdecim object to the standard output.
• firdecim_crcf_clear(q) clears the internal buffer of a firdecim object.
• firdecim_crcf_execute(q,*x,*y,k) computes the output firdecimation of the input sequence \(\vec{x}\) (which is \(D\) samples in size) at the index \(k\) and stores the result in \(y\) .

Filter Delay∞

The delay of the decimator will depend upon the filter coefficients themselves. Normally, an FIR filter has symmetric coefficients and has a length \(2Mm+1\) in which case the output delay is \(Mm\) samples, where \(M\) is the decimation rate and \(m\) is the filter semi-length. But if the filter coefficients are not symmetric or if the filter length follows a different length, the delay will be something different. Unfortunately the decimator cannot compensate for this automatically since it doesn't know the filter response. The delay could even be a fraction of a sample.

If the filter does have a length \(2Mm+1\) then the output delay will be \(m\) samples; this is one of the reasons designing a filter of this length is convenient. If this is the case, you can then just ignore the first \(m\) output samples (e.g. after decimation), and then flush \(m\) blocks of \(M\) samples each through the filter to compensate for that delay.

Example∞

An example of the firdecim interface is listed below.

#include <liquid/liquid.h>

int main() {
    // options
    unsigned int M = 4;         // decimation factor
    unsigned int h_len = 21;    // filter length

    // design filter and create decimator object
    float h[h_len];             // filter coefficients
    firdecim_crcf q = firdecim_crcf_create(M,h,h_len);

    // generate input signal and decimate
    float complex x[M];         // input samples
    float complex y;            // output sample

    // run decimator (repeat as necessary)
    {
        firdecim_crcf_execute(q, x, &y);
    }

    // destroy decimator object
    firdecim_crcf_destroy(q);
}

A more detailed example is given in examples/firdecim_crcf_example.c in the main liquid project directory.