Finite Impulse Response (FIR) Design using Windowed sinc

The ideal low-pass filter has a rectangular response in the frequency domain and an infinite \(\sin(t)/t\) response in the time domain. Because all time-dependent filters must be causal, this type of filter is unrealizable; furthermore, truncating its response results in poor pass-band ripple stop-band rejection. An improvement over truncation is offered by use of a band-limiting window.

Operation

Let the finite impulse response of a filter be defined as

(16)\[h(n) = h_i(n) w(n)\]

where \(w(n)\) is a time-limited symmetric window and \(h_i(n)\) is the impulse response of the ideal filter with a cutoff frequency \(\omega_c\), viz.

(17)\[h_i(n) = \frac{\omega_c}{\pi} \left( \frac{\sin\omega_c n}{\omega_c n} \right), \,\,\,\, \forall n\]

A number of possible windows could be used; the Kaiser window is particularly common due to its systematic ability to trade transition bandwidth for stop-band rejection. The Kaiser window is defined as

(18)\[w(n) = \frac{ I_0\left[\pi\alpha\sqrt{1-\left(\frac{n}{N/2}\right)^2}\right] }{ I_0\left(\pi\alpha\right) } \,\,\,\, -N/2 \leq n \leq N/2, \,\, \alpha \geq 0\]

where \(I_\nu(z)\) is the modified Bessel function of the first kind of order \(\nu\) and \(\alpha\) is a shape parameter controlling the window decay. \(I_\nu(z)\) can be expanded as

(19)\[I_\nu(z) = \left( \frac{z}{2} \right)^\nu \sum_{k=0}^{\infty}{ \frac{ \left(\frac{1}{4}z^2\right)^k }{ k!\Gamma(k+\nu+1) } }\]

The sum in [eqn-filter-firdes-besseli_infinite_sum] converges quickly due to the denominator increasing rapidly, (and in particular for \(\nu=0\) the denominator reduces to \((k!)^2\)) and thus only a few terms are necessary for sufficient approximation. The sum [eqn-filter-firdes-besseli_infinite_sum] converges quickly due to the denominator increasing rapidly, thus only a few terms are necessary for sufficient approximation. For more approximations to \(I_0(z)\) and \(I_\nu(z)\), see [section-math] in the math module. Kaiser gives an approximation for the value of \(\alpha\) to give a particular sidelobe level for the window as {cite:Vaidyanathan:1993((3.2.7))}

(20)\[\begin{split}\alpha = \begin{cases} 0.1102 (A_s - 8.7) & A_s \gt 50 \\ 0.5842 (A_s - 21)^{0.4} & 21 \lt A_s \le 50 \\ 0 & \text{else} \end{cases}\end{split}\]

where \(A_s \gt 0\) is the stop-band attenuation in decibels. This approximation is provided in liquid by the kaiser_beta_As() method, and the length of the filter can be approximated with estimate_req_filter_len() (see [section-filter-misc] for more detail on these methods).

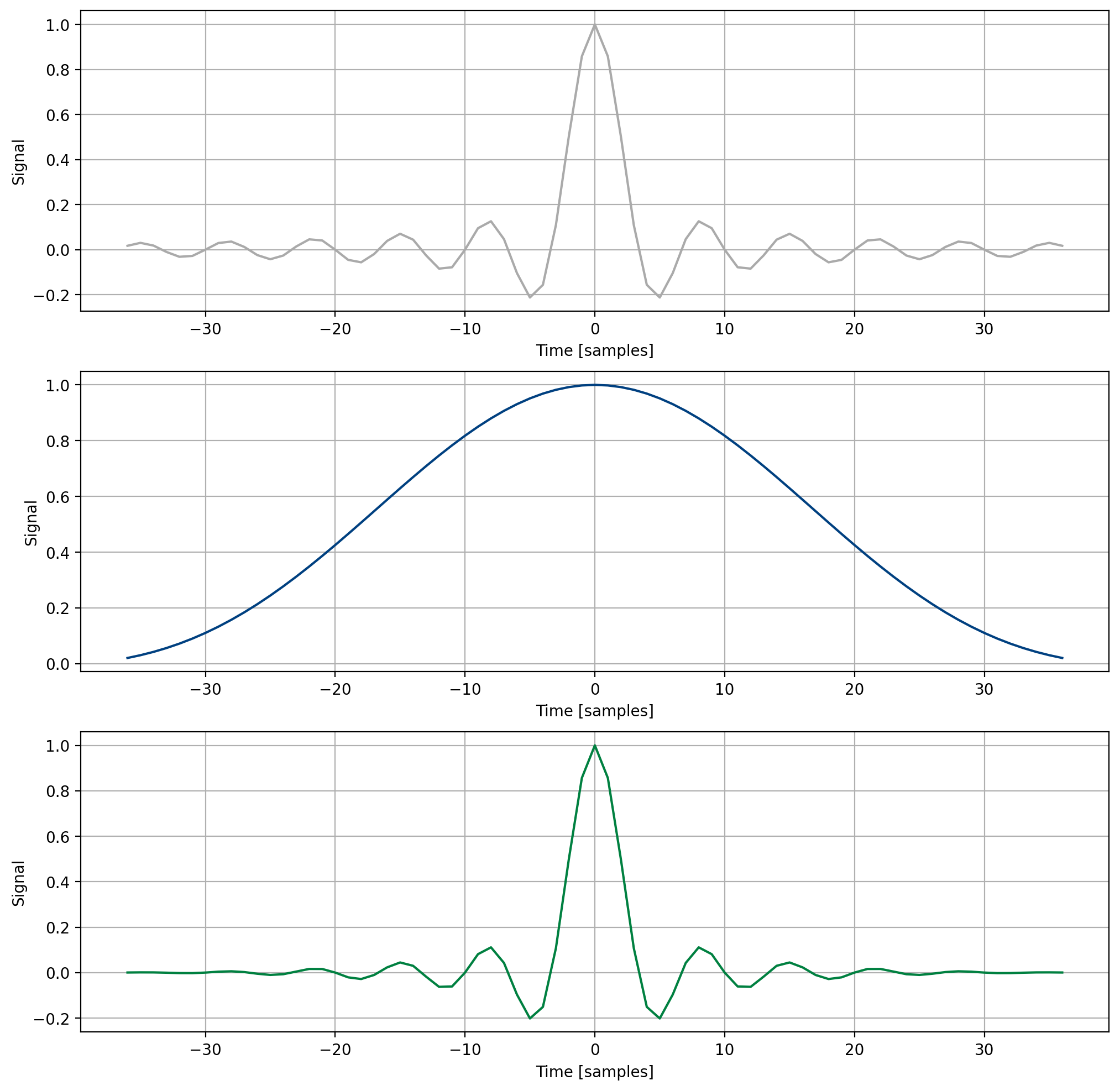
Figure 7 Windowed sinc filter design

Interface

The entire design process is provided in liquid with the firdes_kaiser_window() method which can be invoked as follows:

int liquid_firdes_kaiser(unsigned int _n,
                         float _fc,
                         float _as,
                         float _mu,
                         float *_h);

where _n is the length of the filter (number of samples), _fc is the normalized cutoff frequency (\(0 \leq f_c \leq 0.5\)), _As is the stop-band attenuation in dB (\(A_s \gt 0\)), _mu is the fractional sample offset (\(-0.5 \leq \mu \leq 0.5\)), and *_h is the \(n\)-sample output coefficient array.

Example

Listed below is an example of the firdes_kaiser_window interface.

// demonstrate fir filter design using Kaiser window
#include <stdio.h>
#include <stdlib.h>
#include "liquid.h"

int main(int argc, char*argv[])
{
    // options
    float fc = 0.15f;   // filter cutoff frequency
    float ft = 0.05f;   // filter transition
    float As = 60.0f;   // stop-band attenuation [dB]
    float mu = 0.0f;    // fractional timing offset

    // estimate required filter length and allocate buffer
    unsigned int h_len = estimate_req_filter_len(ft,As);
    float h[h_len];

    // compute filter coefficients and print to stdout
    liquid_firdes_kaiser(h_len,fc,As,mu,h);

    printf("w\n");
    unsigned int i;
    for (i=0; i<h_len; i++)
        printf("%12.8f\n",h[i]);
    return 0;
}

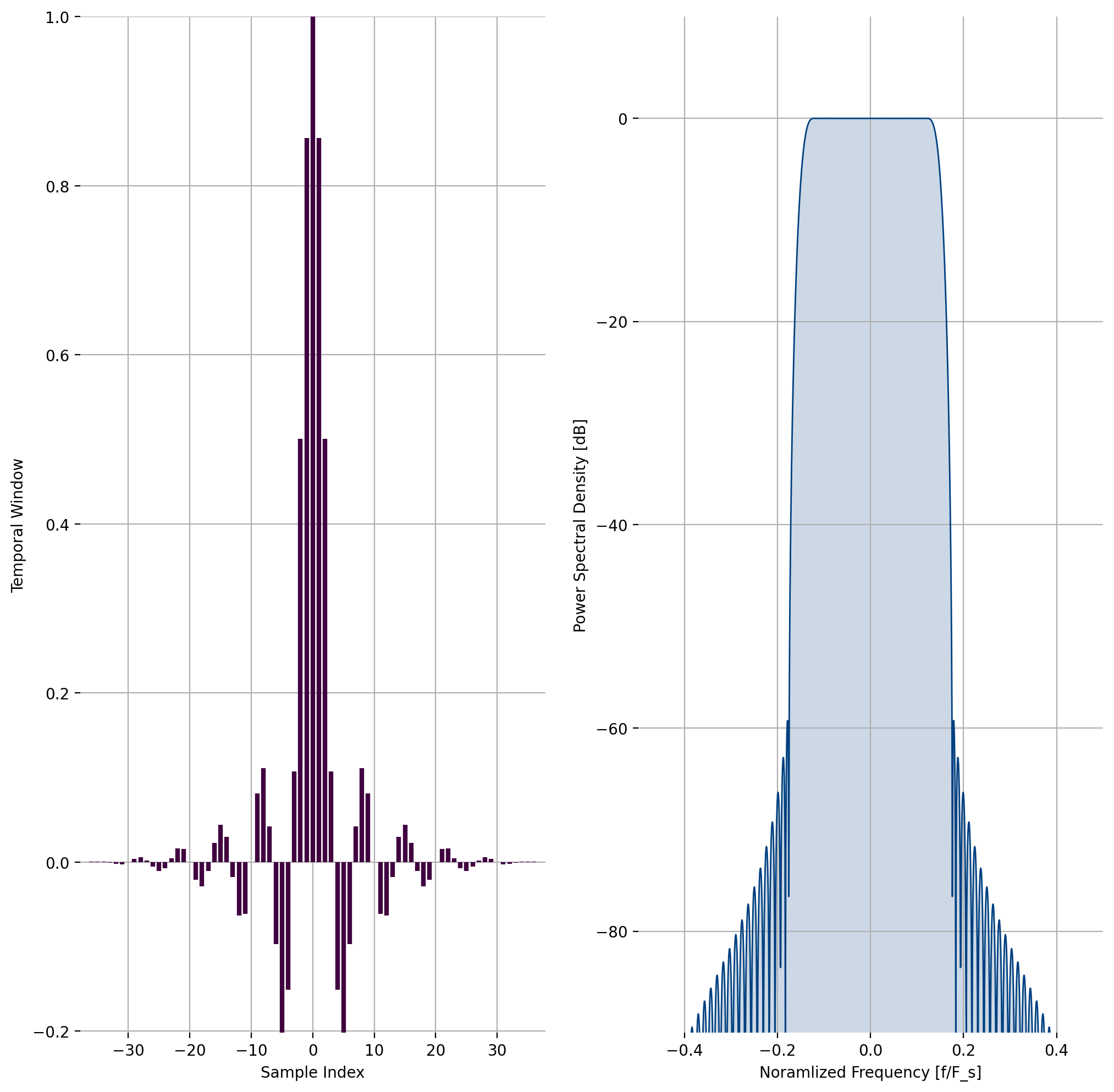
Figure 8 Example of liquid_firdes_kaiser

An example of a low-pass filter design using the Kaiser window can be found in [fig-filter-firdes_kaiser].