Gamma

The gamma distribution has a probability density function defined by

(45)\[\begin{split}f_X(x;\alpha,\beta) = \begin{cases} \frac{ x^{\alpha-1} }{ \Gamma(\alpha) \beta^\alpha } e^{-x / \beta} & x \ge 0 \\ 0 & \text{else}. \end{cases}\end{split}\]

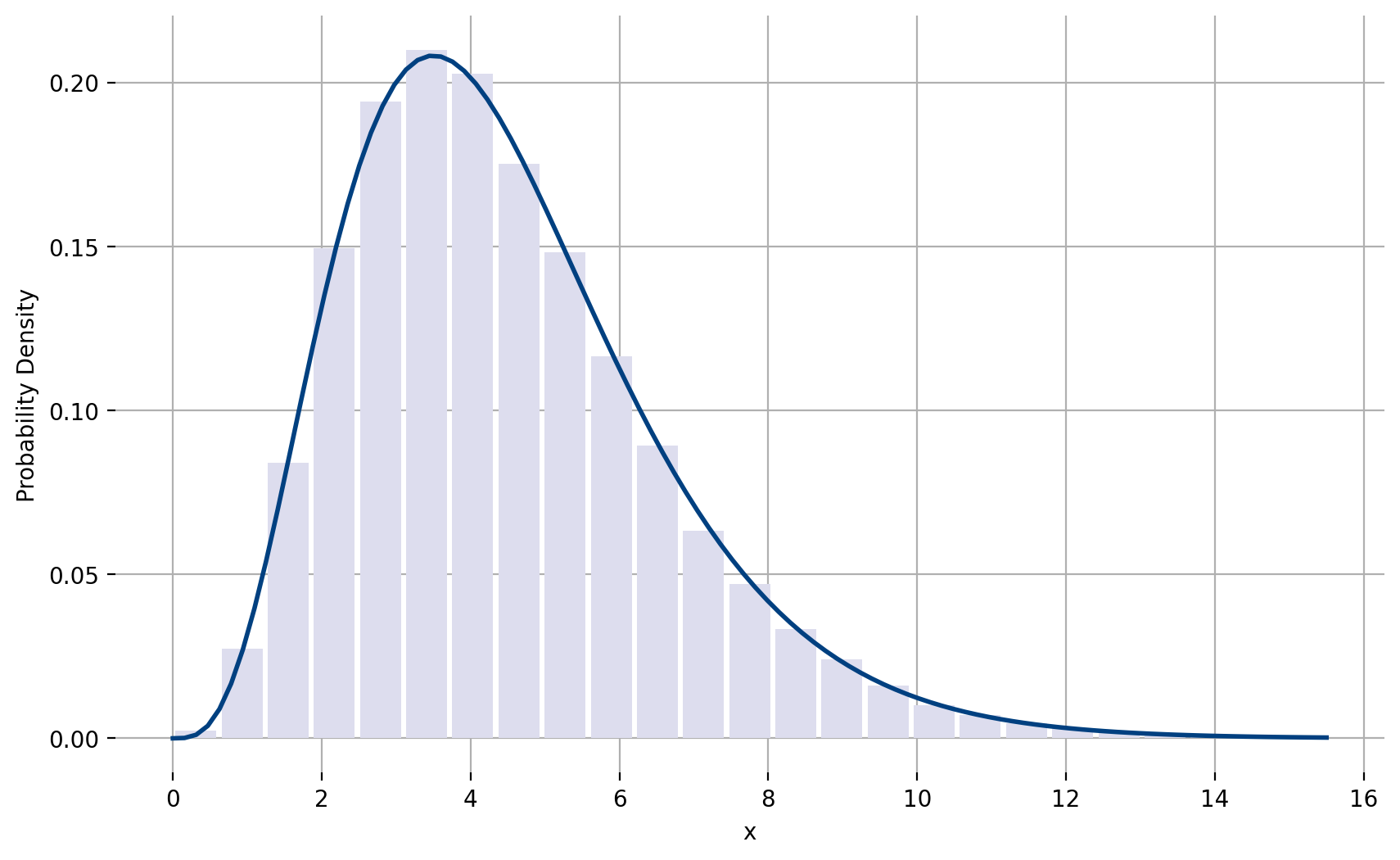
Figure 61 Gamma distribution with \(\alpha=4.5\) and \(\beta=1\)

Interface

Gamma random number generator interface:

// generate gamma random variable
float randgammaf(float _alpha,
                 float _beta);

// compute a gamma probability density
float randgammaf_pdf(float _x,
                     float _alpha,
                     float _beta);

// compute a gamma cumulative distribution
float randgammaf_cdf(float _x,
                     float _alpha,
                     float _beta);