Linear Digital Modulator/Demodulator (modem)

Attention

Re-work for RST, add figures

The modem module implements a set of (mod)ulation/(dem)odulation schemes for encoding information into signals. For the analog modems, samples are encoded according to frequency or analog modulation. For the digital modems, data bits are encoded into symbols representing carrier frequency, phase, amplitude, etc. This section gives a brief overview of linear modulation schemes available in liquid-dsp, and provides a brief description of the interfaces. For non-linear digital modulation, see the documentation on GMSK modem, CP-FSK modem, FSK modem.

Modulation Types

The modem object realizes the linear digital modulation library in which the information from a symbol is encoded into the amplitude and phase of a sample. The modem structure implements a variety of common modulation schemes, including (differential) phase-shift keying, and (quadrature) amplitude-shift keying. The input/output relationship for modulation/demodulation for the modem object is strictly one-to-one and is independent of any pulse shaping, or interpolation.

In general, linear modems demodulate by finding \(\hat{s}\), the closest of \(M\) symbols in the set \(\mathcal{S}_M = \{s_0,s_1,\ldots,s_{M-1}\}\) to the received symbol \(r\), viz

(39)\[\hat{s} = \underset{s_k \in \mathcal{S}_M}{\arg\min} \bigl\{ \| r - s_k \| \bigr\}\]

For arbitrary modulation schemes a linear search over all symbols in \(\mathcal{S}_M\) is required which has a complexity of \(\mathcal{O}(M^2)\); however one may take advantage of symmetries in certain constellations to reduce this to \(\mathcal{O}(\log(M))\).

Table 2 Linear modulation types available in liquid-dsp

Modulation Scheme	Bits/Symbol	Description
LIQUID_MODEM_UNKNOWN	(none)	unknown/unsupported scheme
LIQUID_MODEM_PSK{2,4,8,16,32,64,128,256}	1-8	phase-shift keying
LIQUID_MODEM_DPSK{2,4,8,16,32,64,128,256}	1-8	differential phase-shift keying
LIQUID_MODEM_ASK{2,4,8,16,32,64,128,256}	1-8	amplitude-shift keying
LIQUID_MODEM_QAM{4,8,16,32,64,128,256}	2-8	quadrature amplitude-shift keying
LIQUID_MODEM_APSK{4,8,16,32,64,128,256}	2-8	amplitude/phase-shift keying
LIQUID_MODEM_BPSK	1	binary phase-shift keying
LIQUID_MODEM_QPSK	2	quaternary phase-shift keying
LIQUID_MODEM_OOK	1	on/off keying
LIQUID_MODEM_SQAM32	5	“square” 32-QAM
LIQUID_MODEM_SQAM128	7	“square” 128-QAM
LIQUID_MODEM_V29	4	V.29 star modem
LIQUID_MODEM_ARB16OPT	4	optimal 16-QAM
LIQUID_MODEM_ARB32OPT	5	optimal 32-QAM
LIQUID_MODEM_ARB64OPT	6	optimal 64-QAM
LIQUID_MODEM_ARB128OPT	7	optimal 128-QAM
LIQUID_MODEM_ARB256OPT	8	optimal 256-QAM
LIQUID_MODEM_ARB64VT	6	Virginia Tech logo
LIQUID_MODEM_ARB	1-8	arbitrary signal constellation

Dynamic-sized Modulation Types

Phase-shift Keying (PSK)

With phase-shift keying the information is stored in the absolute phase of the modulated signal. This means that each of \(M=2^m\) symbols in the constellation are equally spaced around the unit circle.

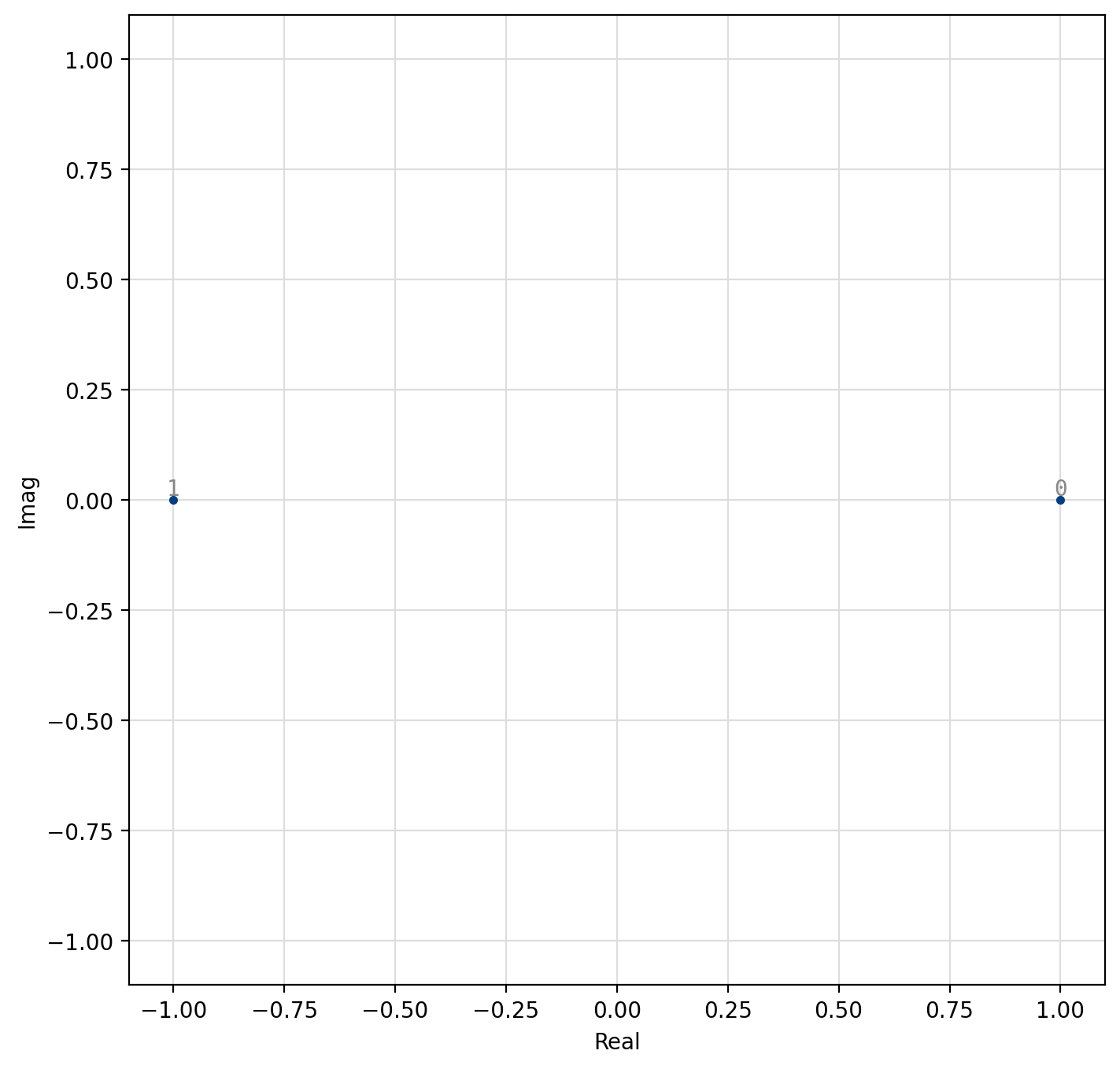
Figure 29 2-PSK (generic BPSK)

Figure 30 4-PSK (generic QPSK)

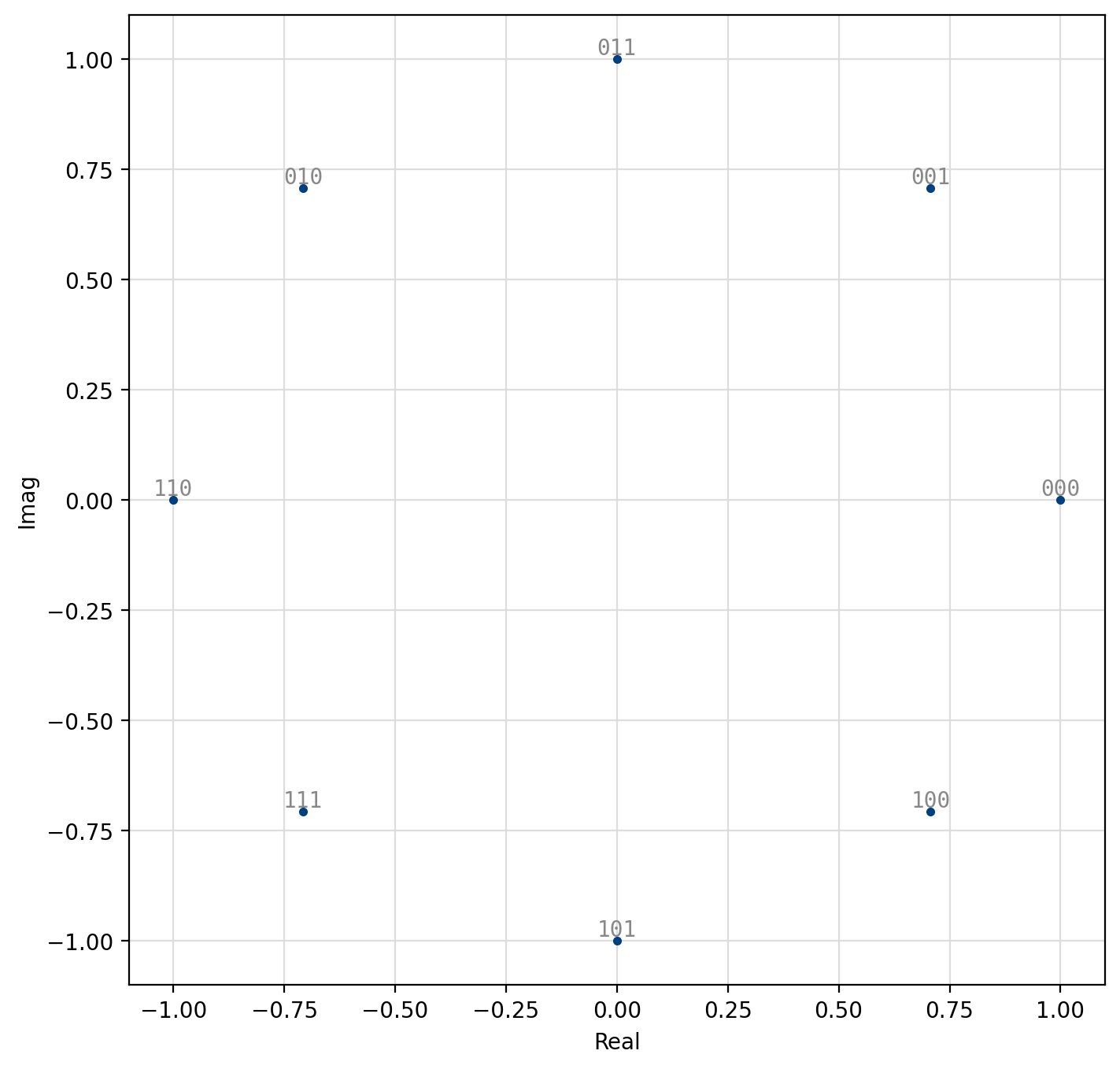
Figure 31 8-PSK

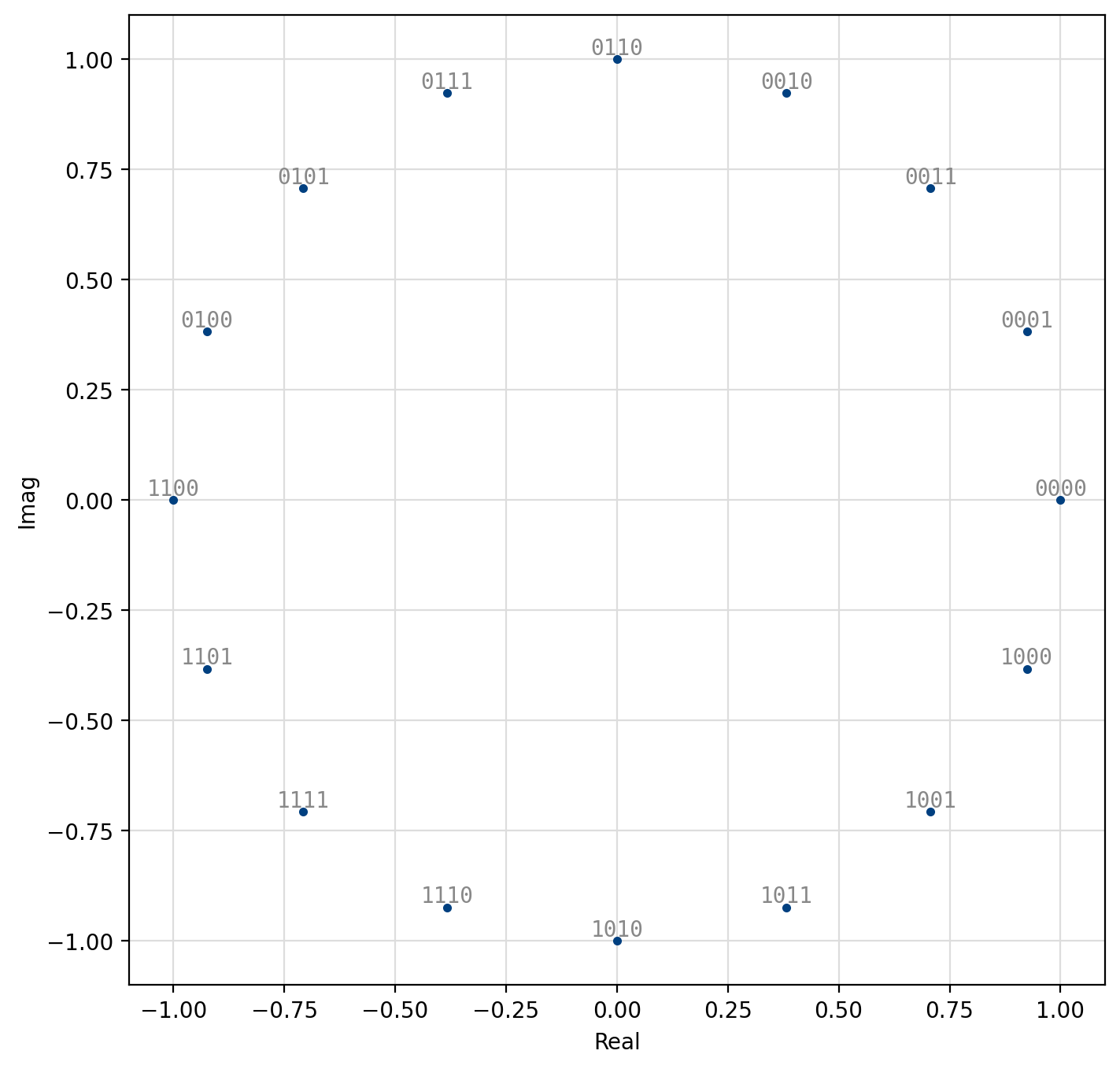
Figure 32 16-PSK

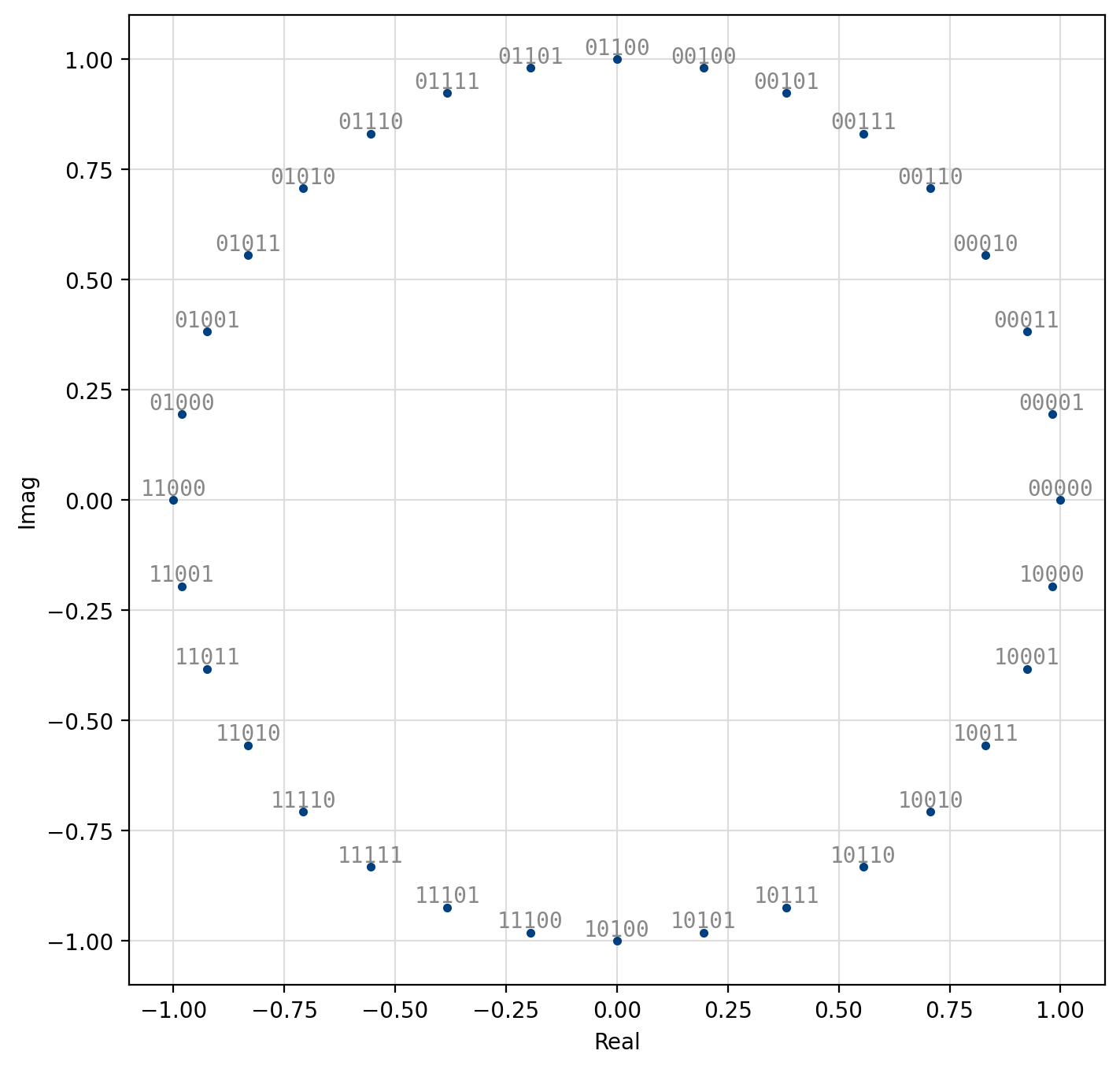
Figure 33 32-PSK

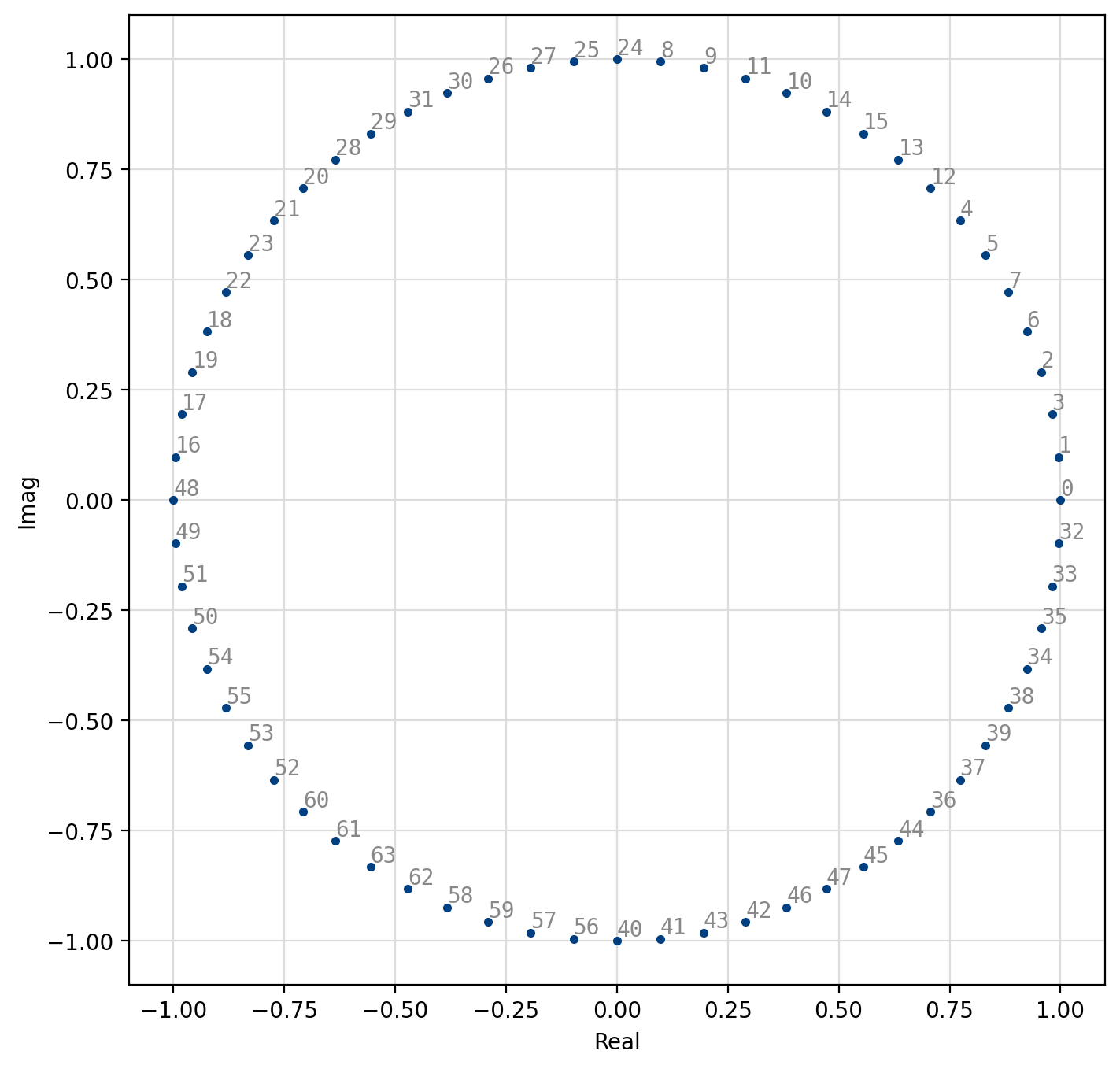
Figure 34 64-PSK

[fig-modem-psk] depicts the constellation of PSK up to \(M=16\) with the bits gray encoded. While liquid-dsp supports up to \(M=256\), values greater than \(M=32\) are typically avoided due to error rates for practical signal-to-noise ratios. For an \(M\)-symbol constellation, the \(k^{th}\) symbol is

\[s_k = e^{j 2 \pi k/M}\]

where \(k \in \{0,1,\ldots,M-1\}\). Specific schemes include BPSK (\(M=2\)),

\[\begin{split}s_k = e^{j \pi k} = \begin{cases} +1 & k=0 \\ -1 & k=1 \end{cases}\end{split}\]

and QPSK (\(M=4\))

\[s_k = e^{j\left(\pi k/4 + \frac{\pi}{4}\right)}\]

Demodulation is performed independent of the signal amplitude for coherent PSK.

Differential Phase-shift Keying (DPSK)

Differential PSK (DPSK) encodes information in the phase change of the carrier. Like regular PSK demodulation is performed independent of the signal amplitude; however because the data are encoded using phase transitions rather than absolute phase, the receiver does not have to know the absolute phase of the transmitter. This allows the receiver to demodulate incoherently, but at a quality degradation of 3dB. As such the \(n^{th}\) transmitted symbol \(k(n)\) depends on the previous symbol, viz

\[s_k(n) = \exp\left\{ \frac{ j 2 \pi \Bigl(k(n) - k(n-1)\Bigr) } { M } \right\}\]

Amplitude/Phase-shift Keying (APSK)

Amplitude/phase-shift keying (APSK) is a specific form of quadrature amplitude modulation where constellation points lie on concentric circles. The constellation points are further apart than those of PSK/DPSK, resulting in an improved error performance. Furthermore the phase recovery for APSK is improved over regular QAM as the constellation points are less sensitive to phase noise. This improvement comes at the cost of an increased computational complexity at the receiver. Demodulation follows as a two-step process: first, the amplitude of the received signal is evaluated to determine in which level (“ring”) the transmitted symbol lies. Once the level is determined, the appropriate symbol is chosen based on its phase, similar to PSK demodulation. Demodulation of APSK consumes slightly more clock cycles than the PSK and QAM demodulators.

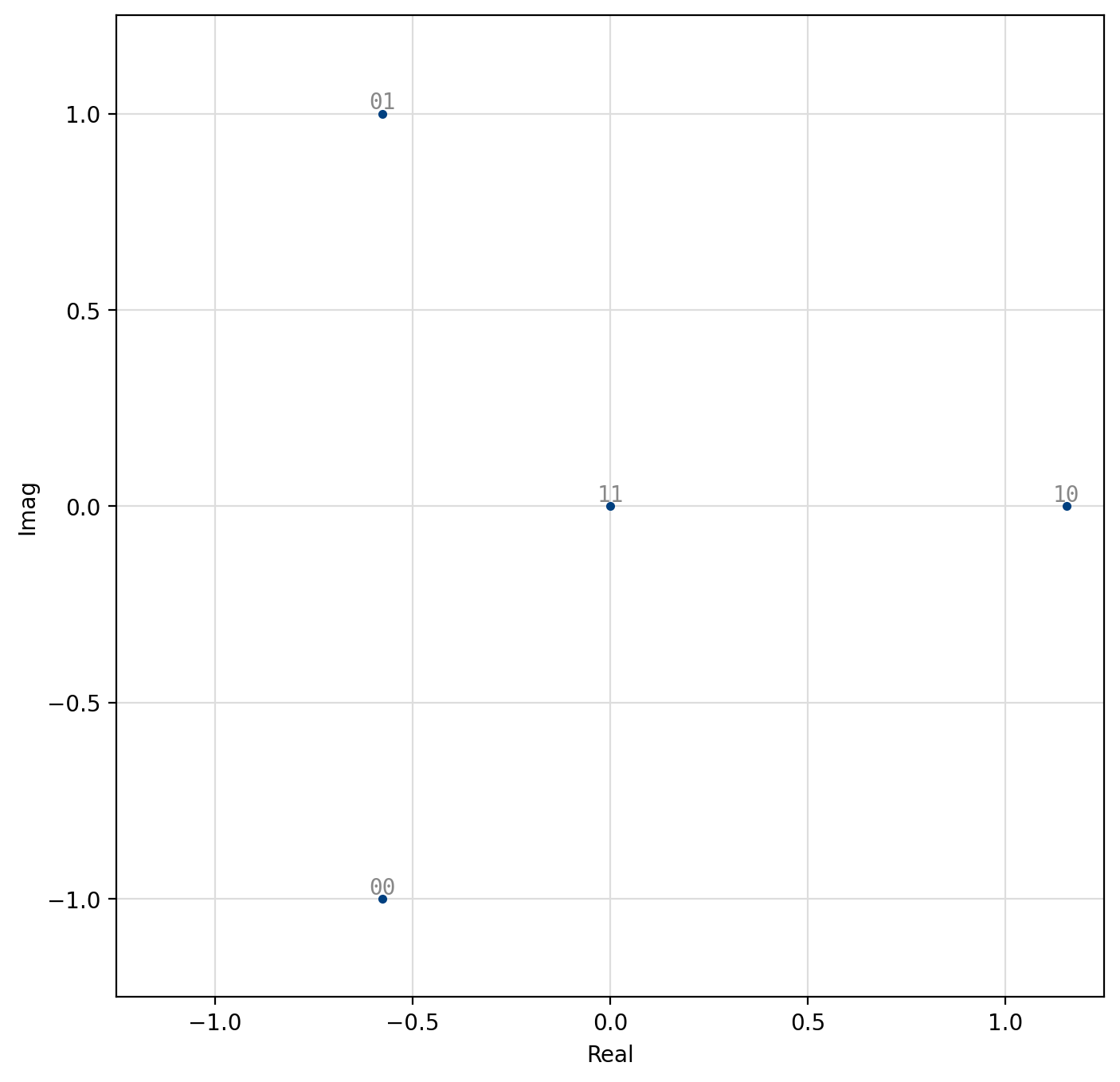
Figure 35 4-APSK (1,3)

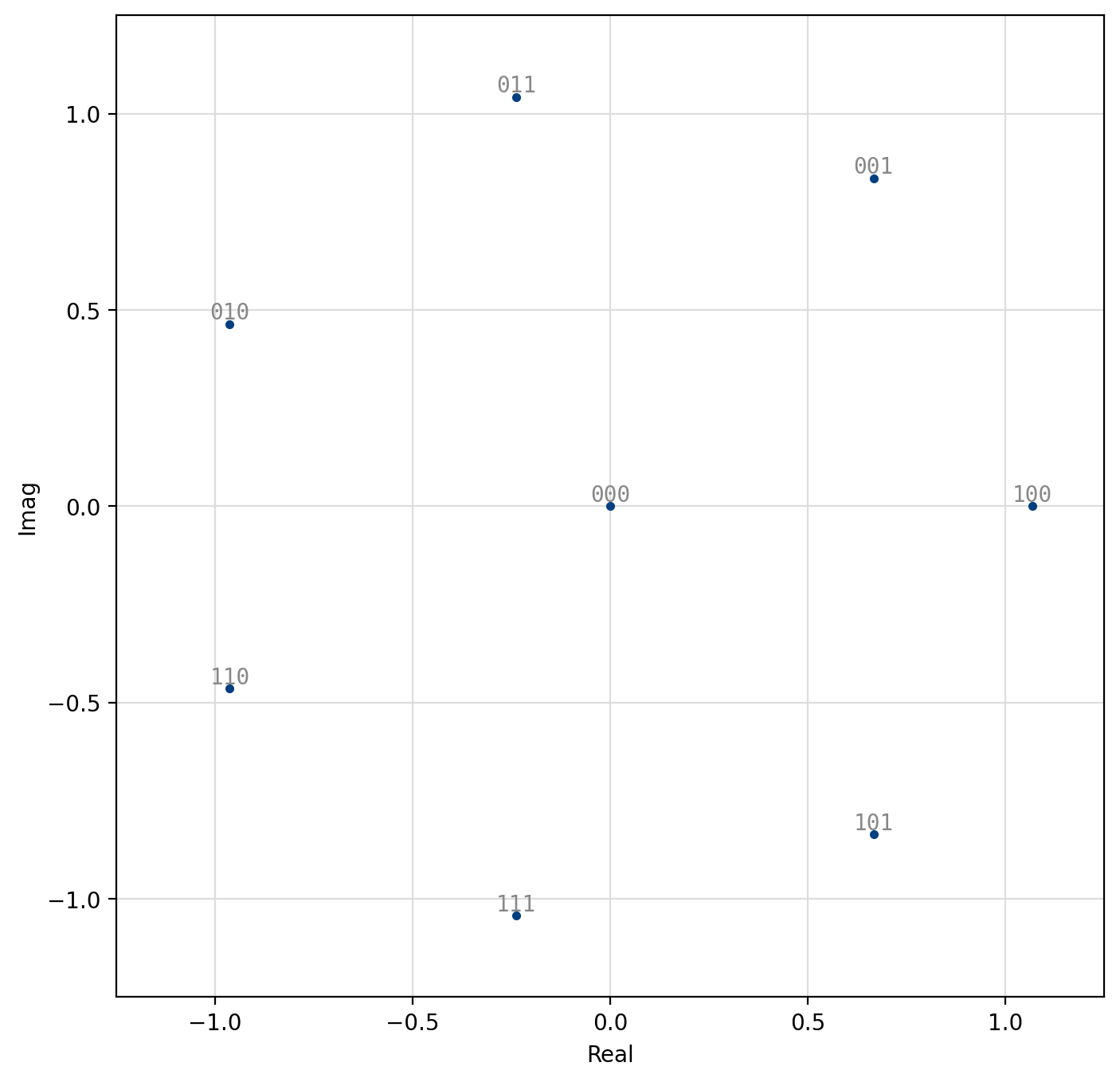
Figure 36 8-PSK (1,7)

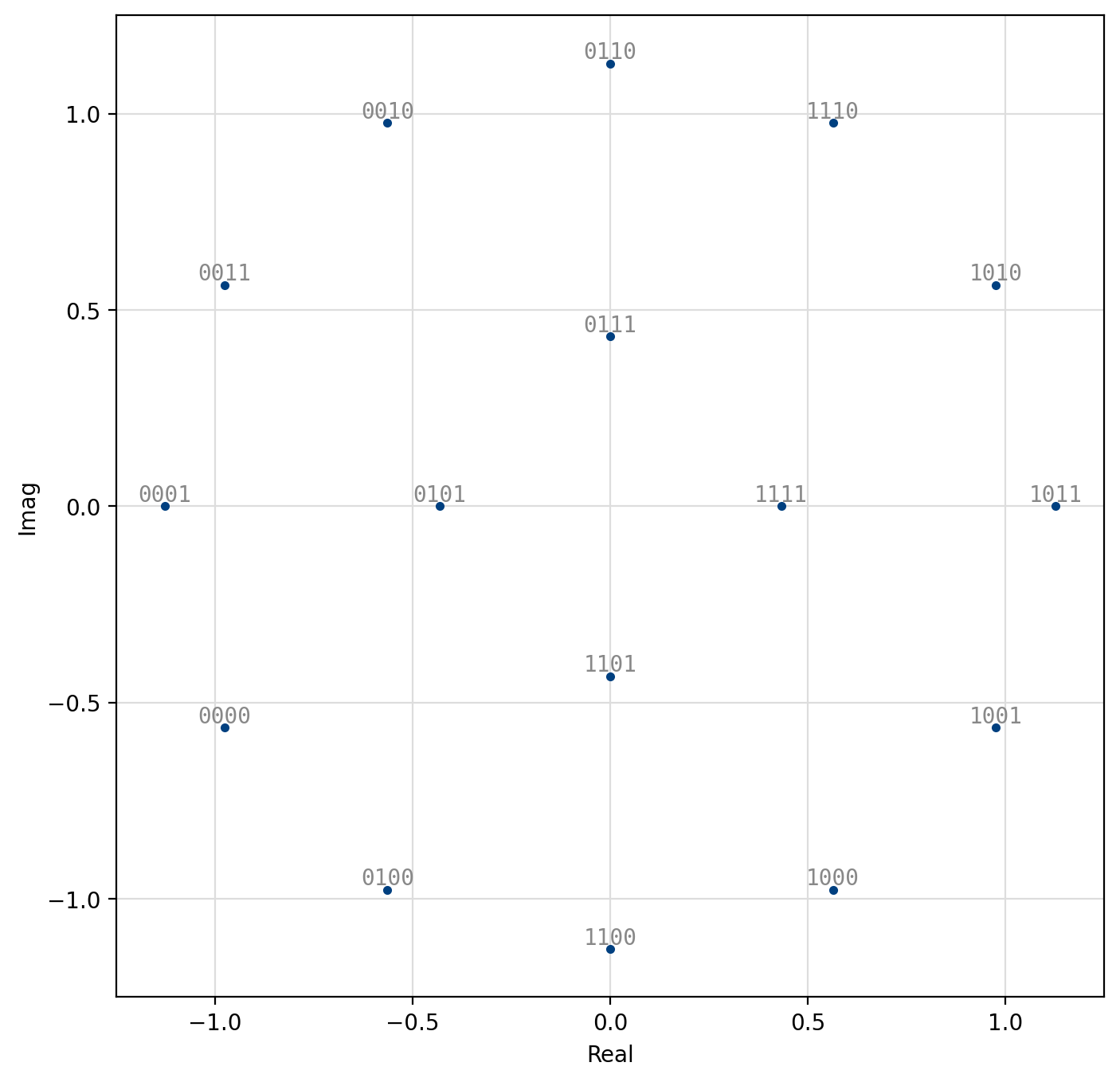
Figure 37 16-APSK (4,12)

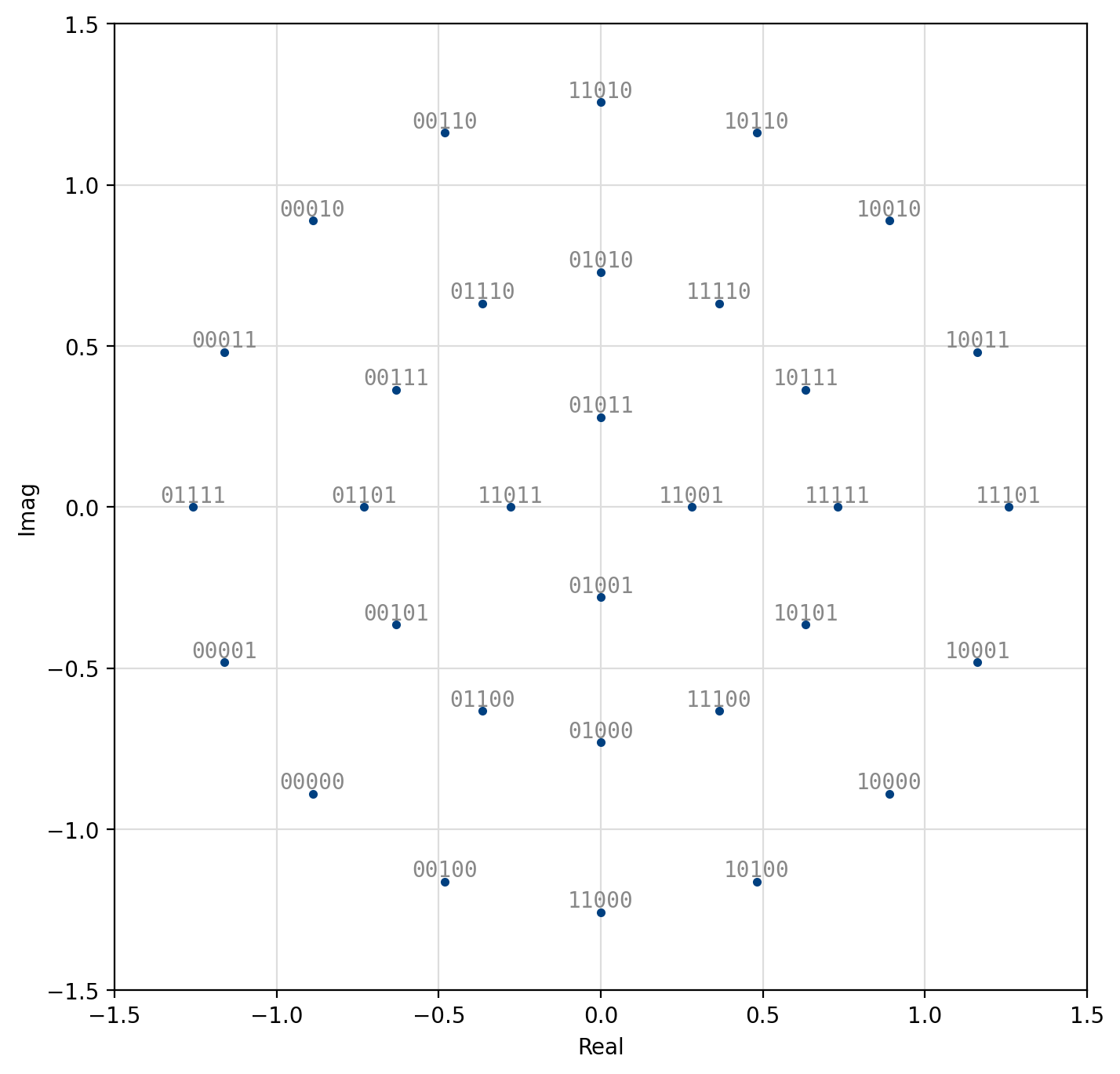
Figure 38 32-APSK (4,12,16)

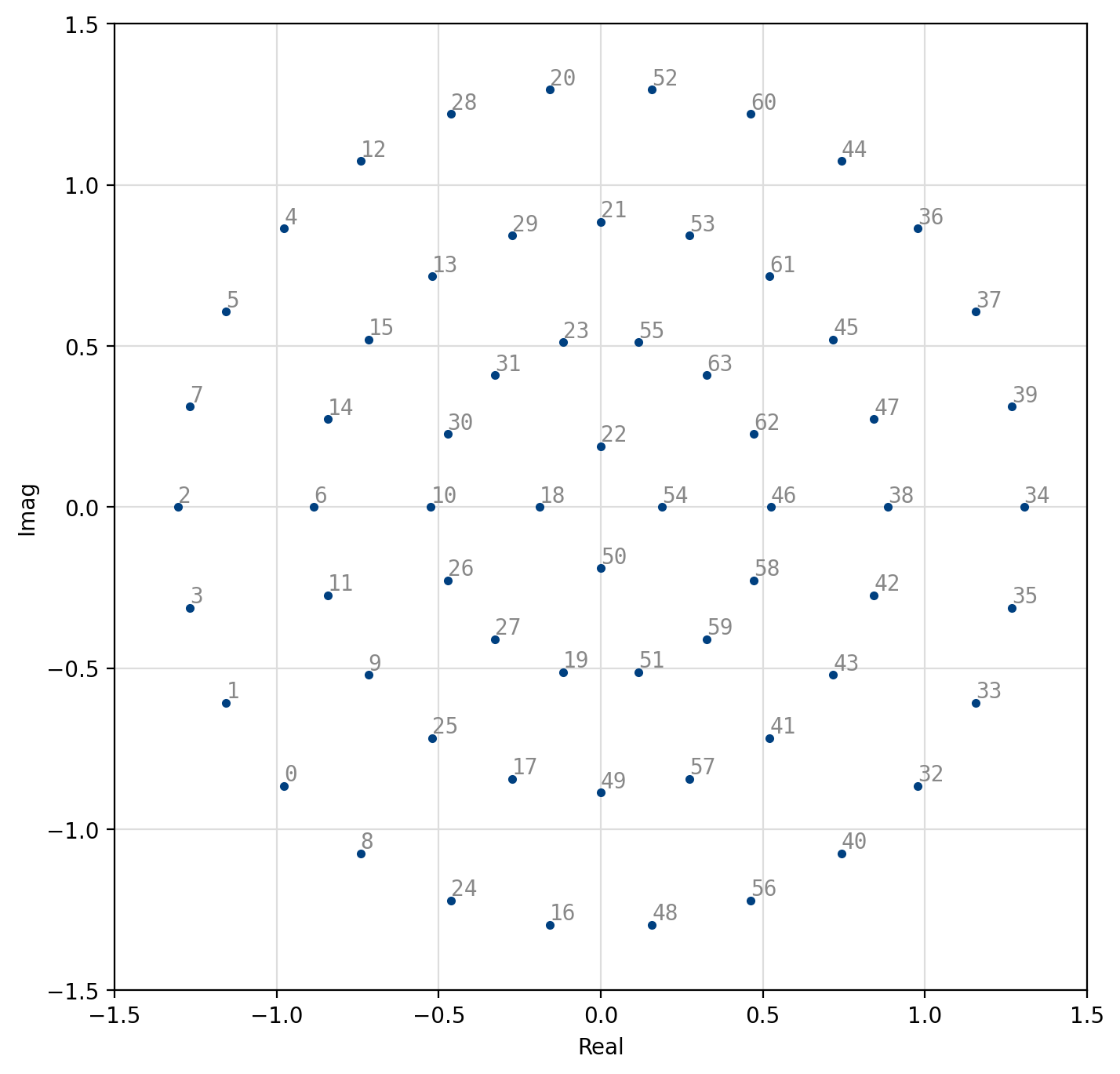
Figure 39 64-APSK (4,14,20,26)

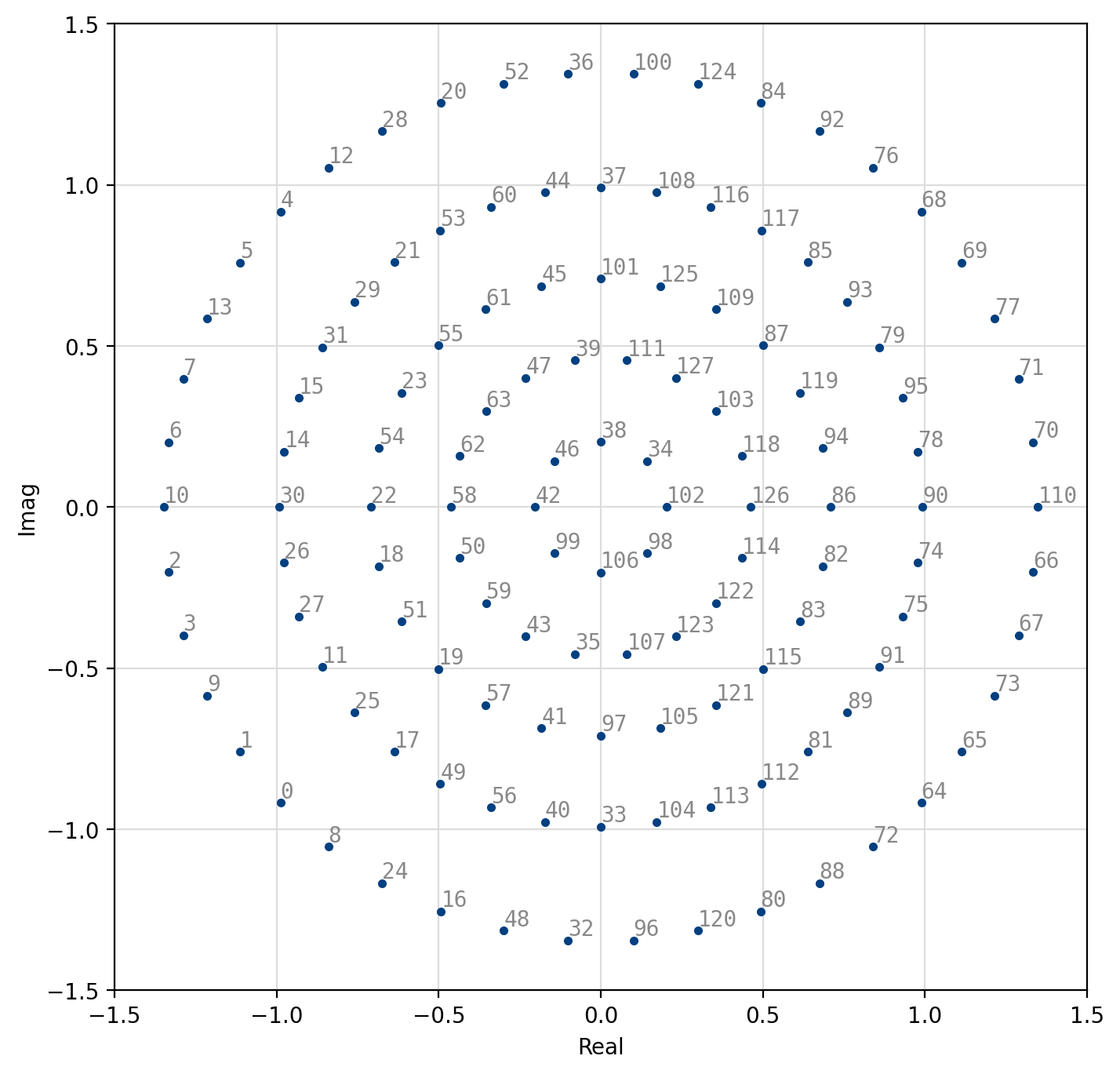
Figure 40 128-APSK (8,18,24,36,42)

[fig-modem-apsk] depicts the available APSK signal constellations for \(M\) up to 128. The constellation points and bit mappings have been optimized to minimize the bit error rate in 10 dB SNR.

Amplitude-shift Keying (ASK)

Amplitude-shift keying (ASK) is a simple form of amplitude modulation by which the information is encoded entirely in the in-phase component of the baseband signal. The encoded symbol is simply

\[s_k = \alpha \bigl( 2 k - M - 1 \bigr)\]

where \(\alpha\) is a scaling factor to ensure \(E\{s_k^2\}=1\),

\[\begin{split}\alpha = \begin{cases} 1 & M=2 \\ 1/\sqrt{5} & M=4 \\ 1/\sqrt{21} & M=8 \\ 1/\sqrt{85} & M=16 \\ 1/\sqrt{341} & M=32 \\ \sqrt{3}/M & M \gt 32 \end{cases}\end{split}\]

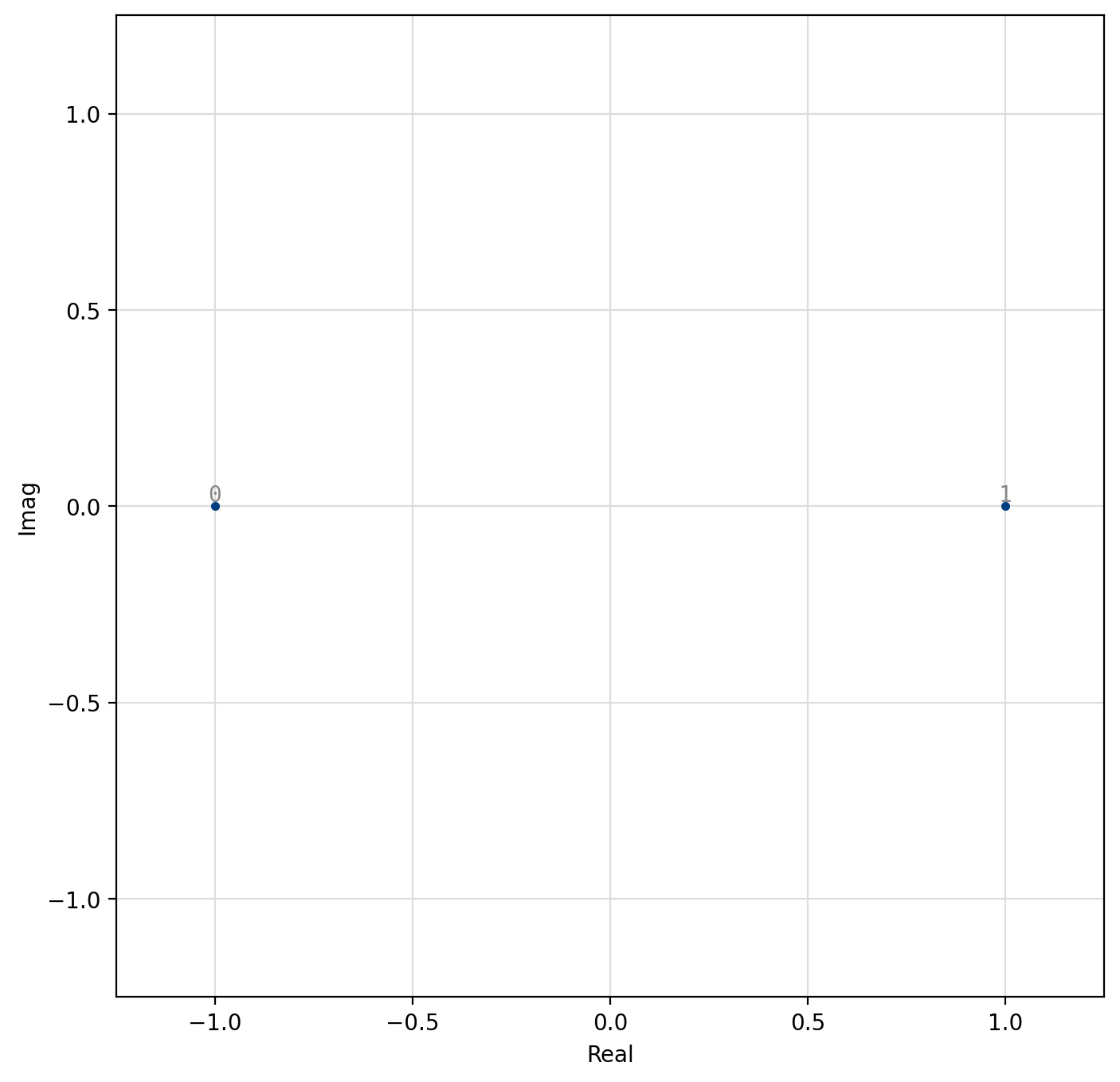
Figure 41 2-ASK

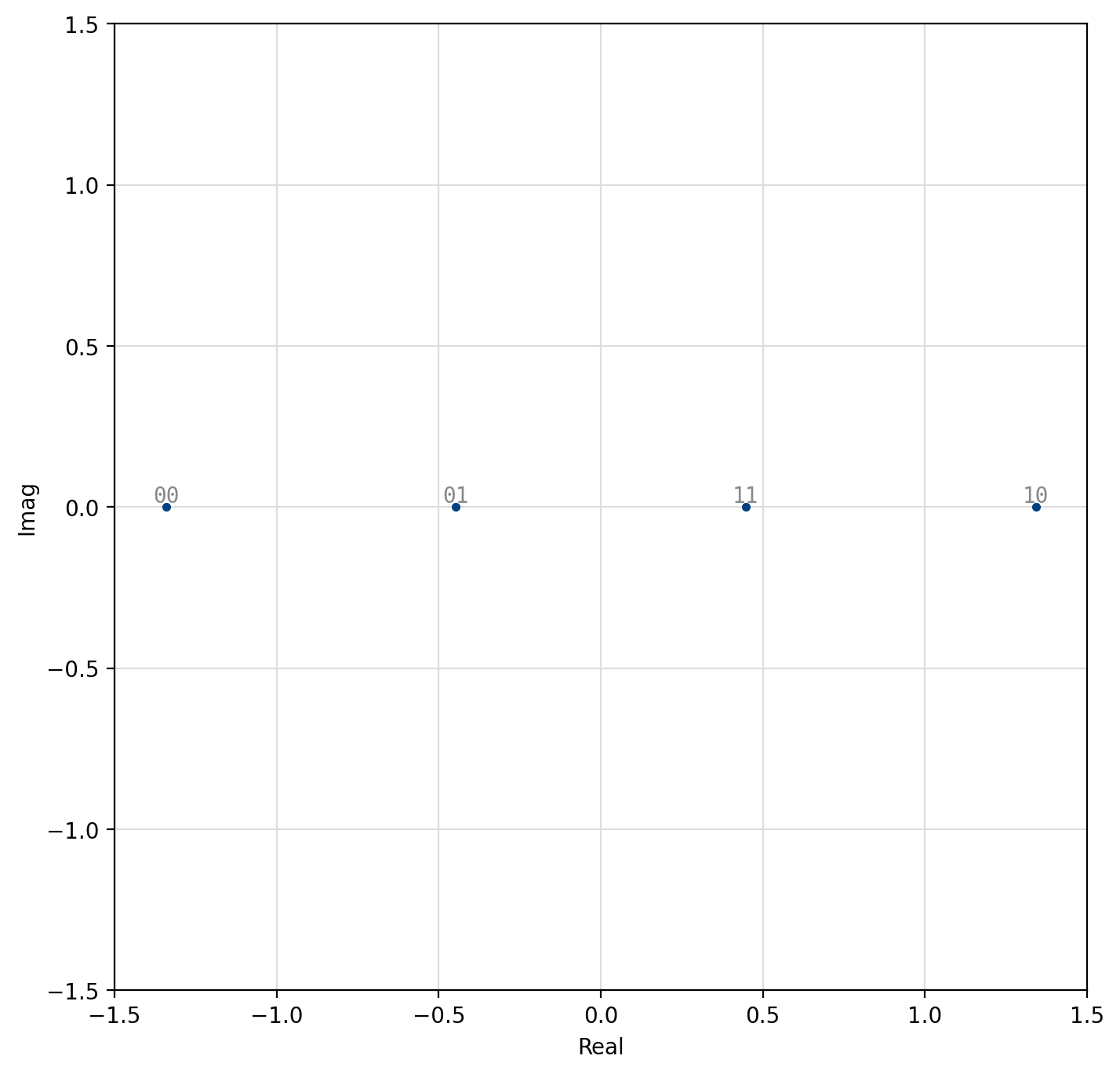
Figure 42 4-ASK

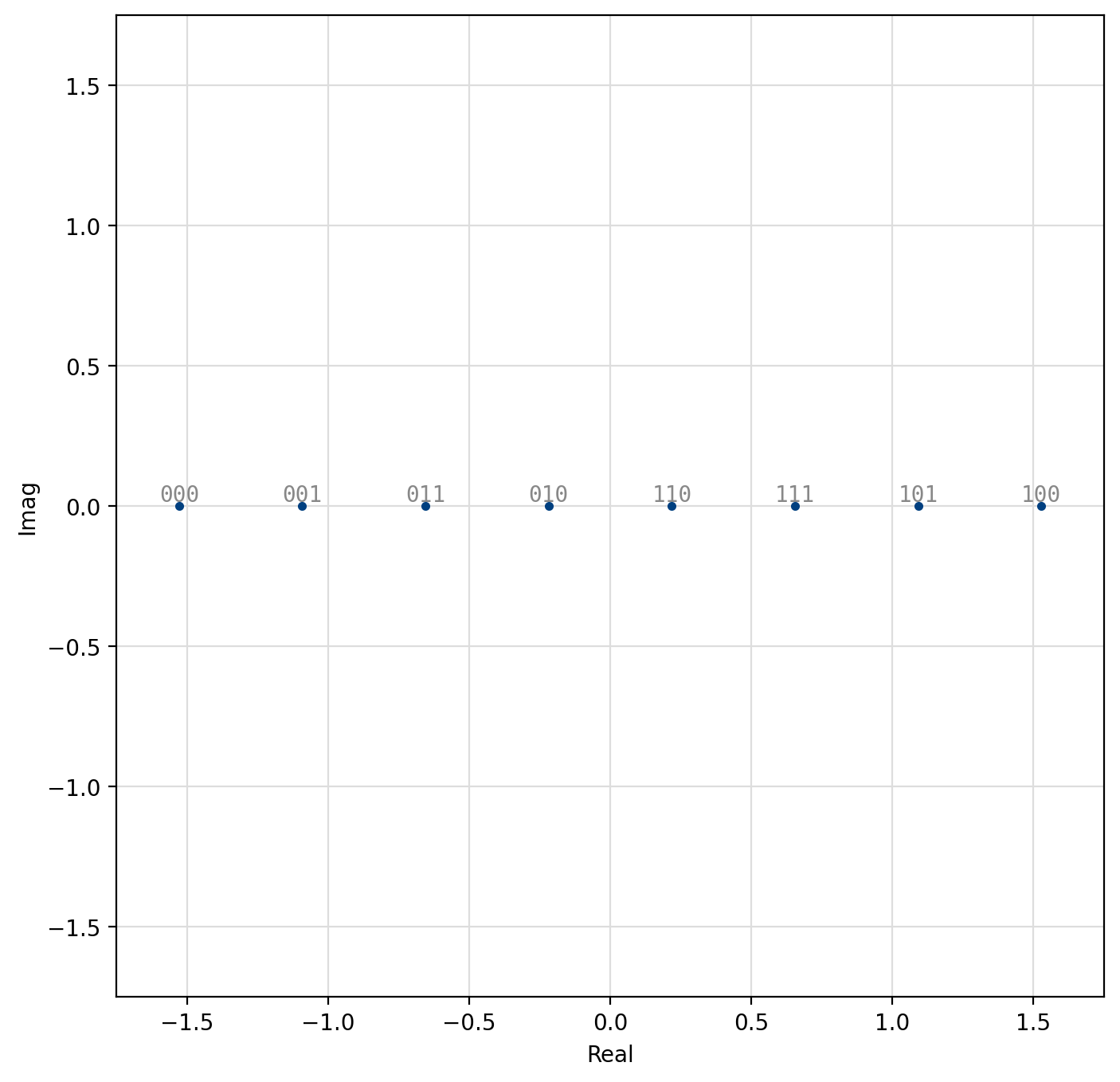
Figure 43 8-ASK

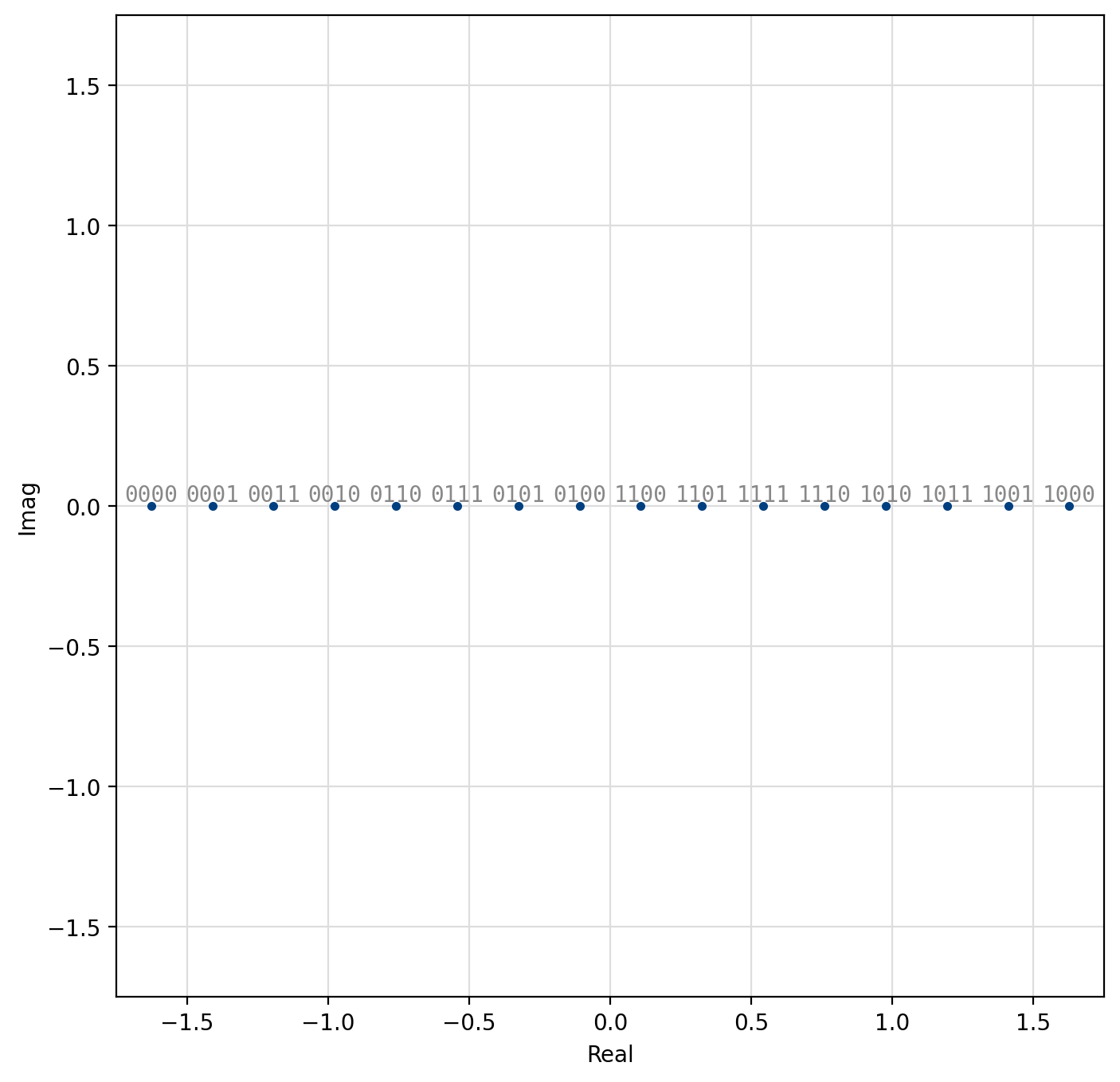
Figure 44 16-ASK

[fig-modem-ask] depicts the ASK constellation map for \(M\) up to 16. Due to the poor error rate performance of ASK values of \(M\) greater than 16 are not recommended.

Quadrature Amplitude Modulation (QAM)

Also known as quadrature amplitude-shift keying, QAM modems encode data using both the in-phase and quadrature components of a signal amplitude. In fact, the symbol is split into independent in-phase and quadrature symbols which are encoded separately as LIQUID_MODEM_ASK symbols. Gray encoding is applied to both the I and Q symbols separately to help ensure minimal bit changes between adjacent samples across both in-phase and quadrature-phase dimensions. This is made evident in [fig-modem-qam-64] where one can see that the first three bits of the symbol encode the in-phase component of the sample, and the last three bits encode the quadrature component of the sample. We may formally describe the encoded sample is

\[s_k = \alpha \Bigl\{ ( 2 k_i - M_i - 1 ) + j(2 k_q - M_q - 1) \Bigr\}\]

where \(k_i\) is the in-phase symbol, \(k_q\) is the quadrature symbol, \(M_i = 2^{m_i}\) and \(M_q = 2^{m_q}\), are the number of respective in-phase and quadrature symbols, \(m_i=\lceil \log_2(M) \rceil\) and \(m_q=\lfloor \log_2(M) \rfloor\) are the number of respective in-phase and quadrature bits, and \(\alpha\) is a scaling factor to ensure \(E\{s_k^2\}=1\),

\[\begin{split}\alpha = \begin{cases} 1/\sqrt{2} & M=4 \\ 1/\sqrt{6} & M=8 \\ 1/\sqrt{10} & M=16 \\ 1/\sqrt{26} & M=32 \\ 1/\sqrt{42} & M=64 \\ 1/\sqrt{106} & M=128 \\ 1/\sqrt{170} & M=256 \\ 1/\sqrt{426} & M=512 \\ 1/\sqrt{682} & M=1024 \\ 1/\sqrt{1706} & M=2048 \\ 1/\sqrt{2730} & M=4096 \\ \sqrt{2/M} & \text{else} \end{cases}\end{split}\]

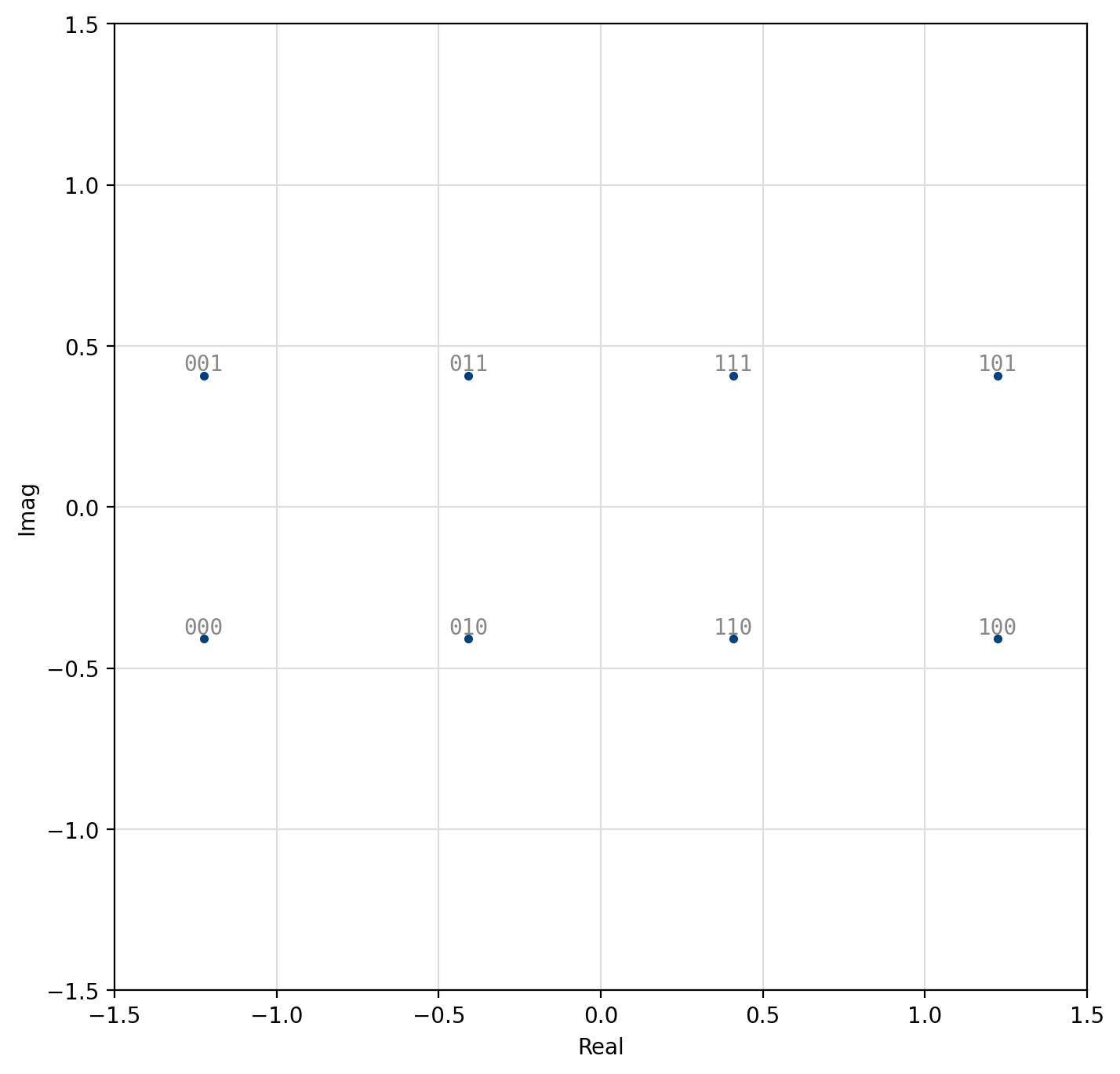
Figure 45 8-QAM constellation

Figure 46 16-QAM constellation

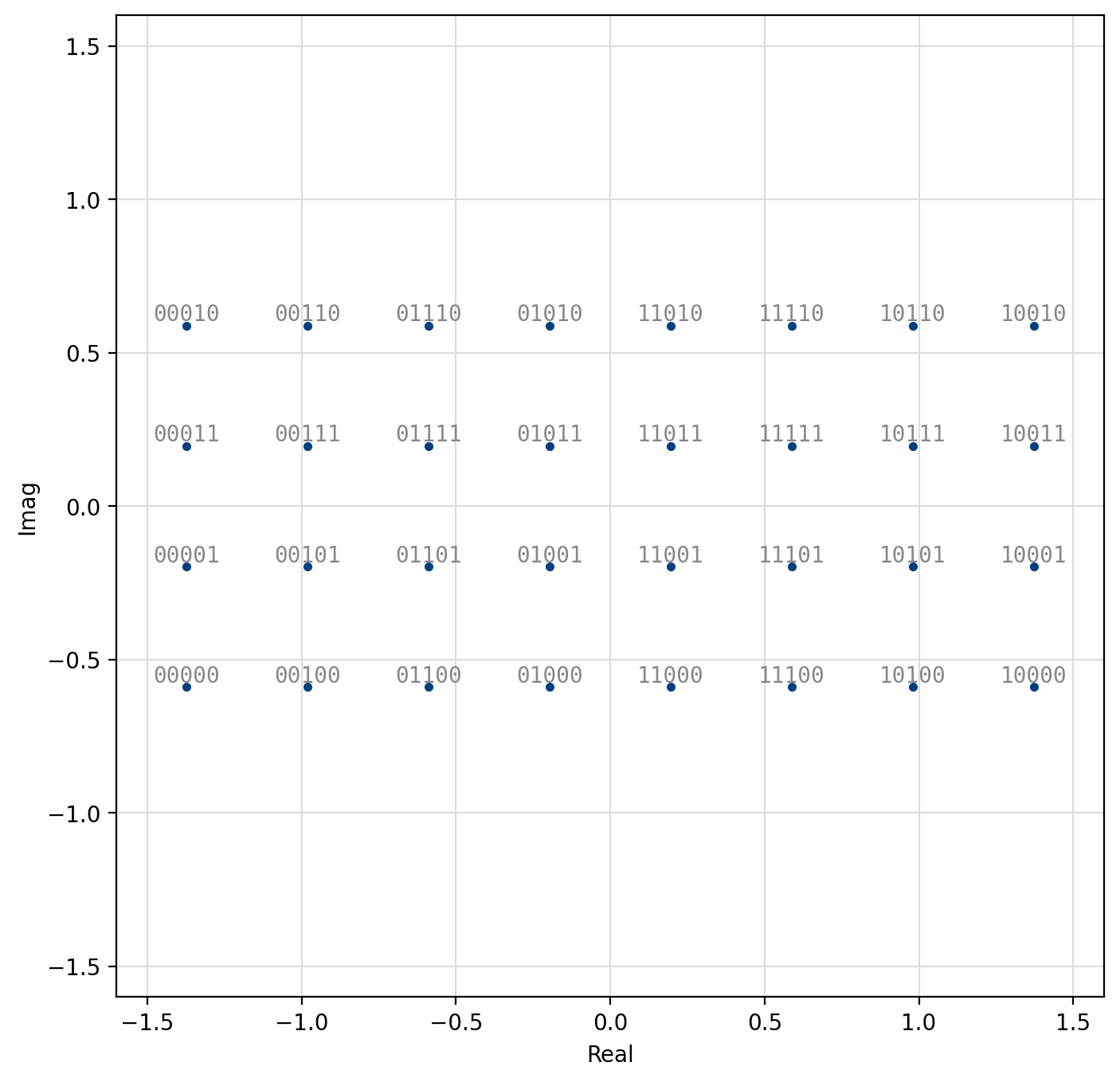
Figure 47 32-QAM constellation

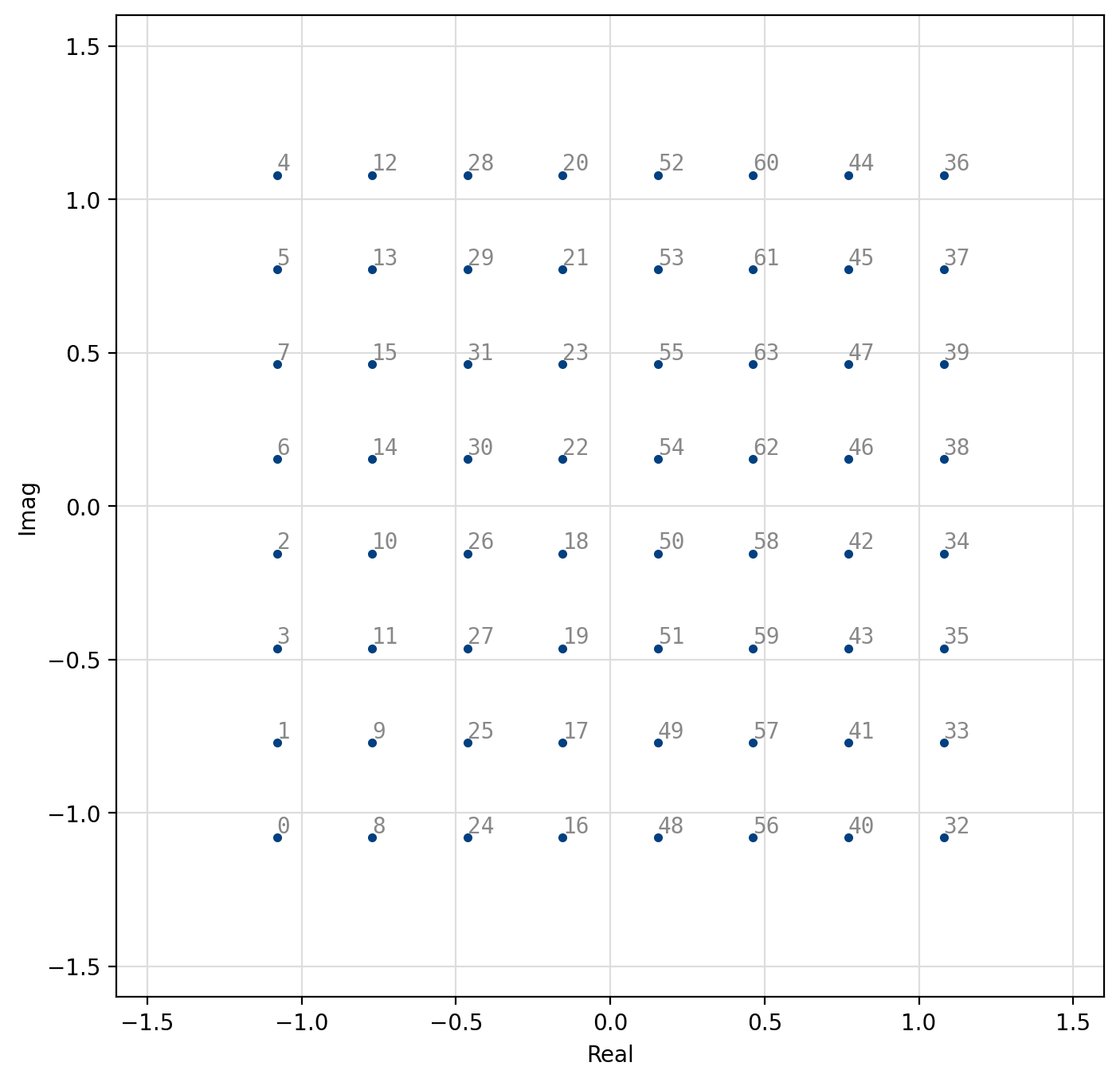
Figure 48 64-QAM constellation

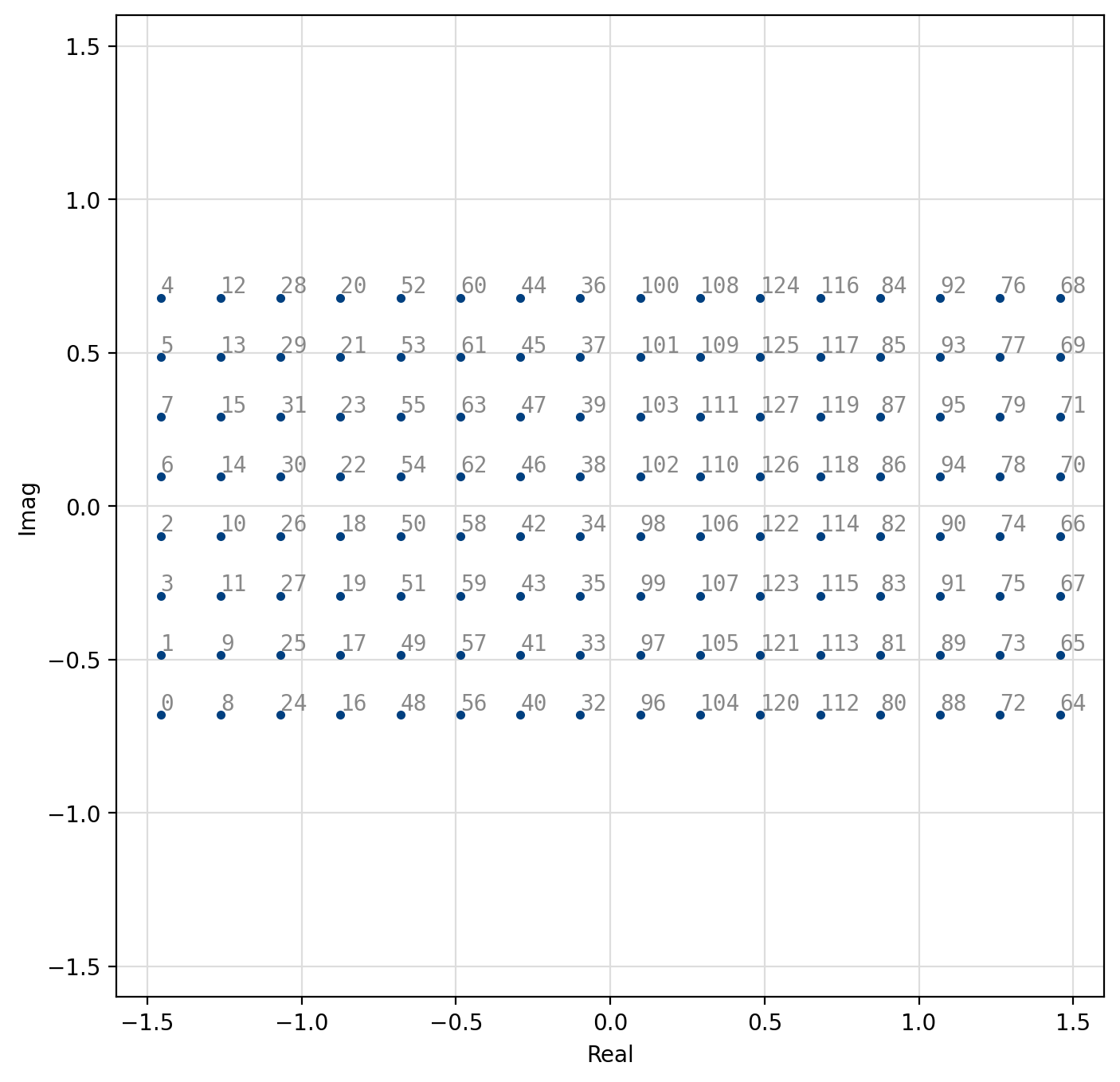
Figure 49 128-QAM constellation

Figure 50 256-QAM constellation

[fig-modem-qam] depicts the arbitrary rectangular QAM modem constellation maps for \(M\) up to 256. Notice that all the symbol points are gray encoded to minimize bit errors between adjacent symbols.

Fixed-size Modulation Types

BPSK, QPSK, etc.

Arbitrary Modulation Types

liquid-dsp also allows the user to create their own modulation schemes by designating the full signal constellation. The penalty for defining a constellation as an arbitrary set of points is that it cannot be decoded systematically. All of the previous modulation schemes have the benefit of being very fast to decode, and do not necessitate searching over the entire constellation space to find the nearest symbol. An example interface for generating a pair of arbitrary modems is listed below.

Several pre-defined arbitrary signal constellations are available, including optimal QAM constellations, and some other fun (but perhaps not so useful) modulation schemes.

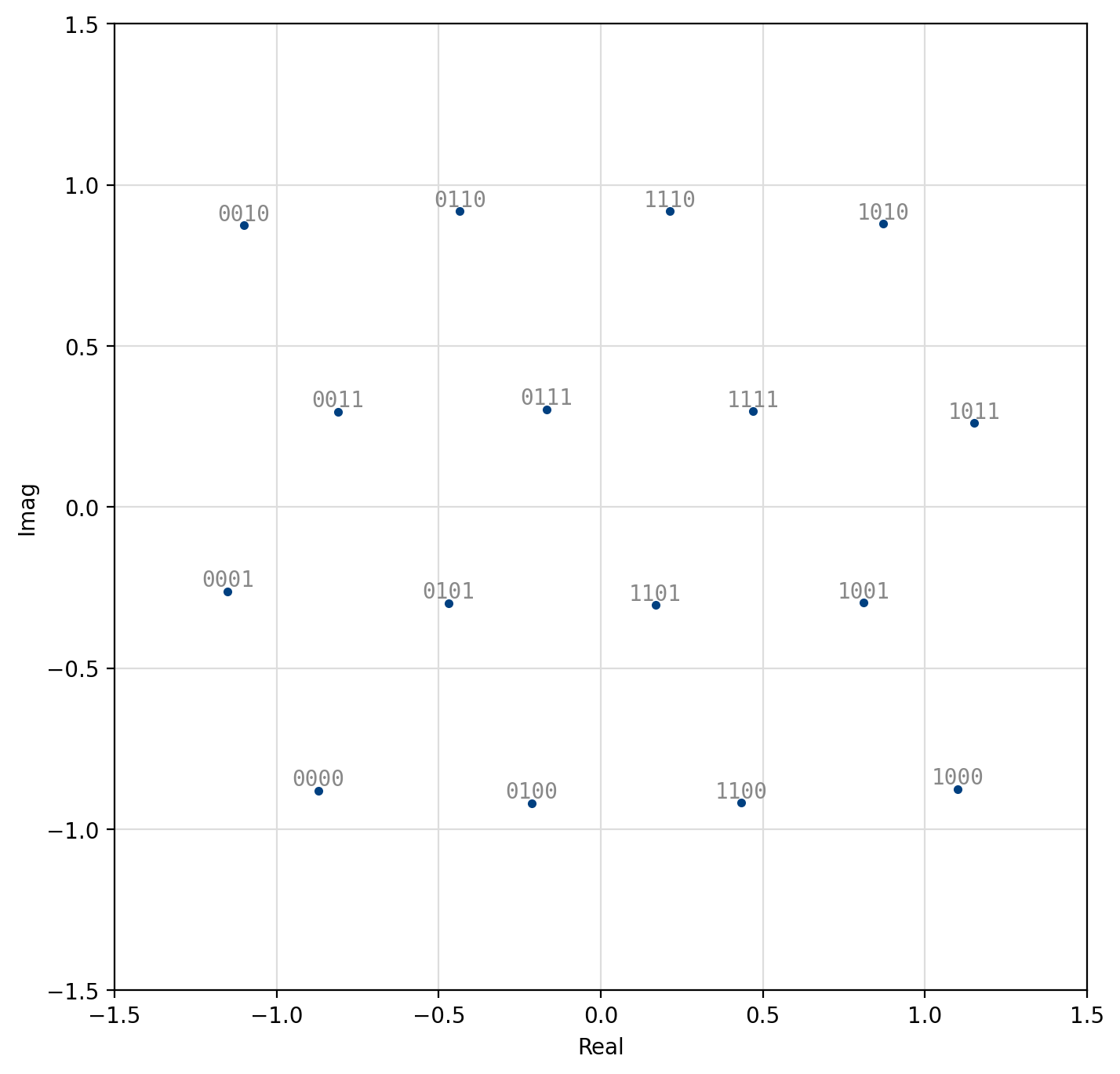
Figure 51 Optimal 16-QAM

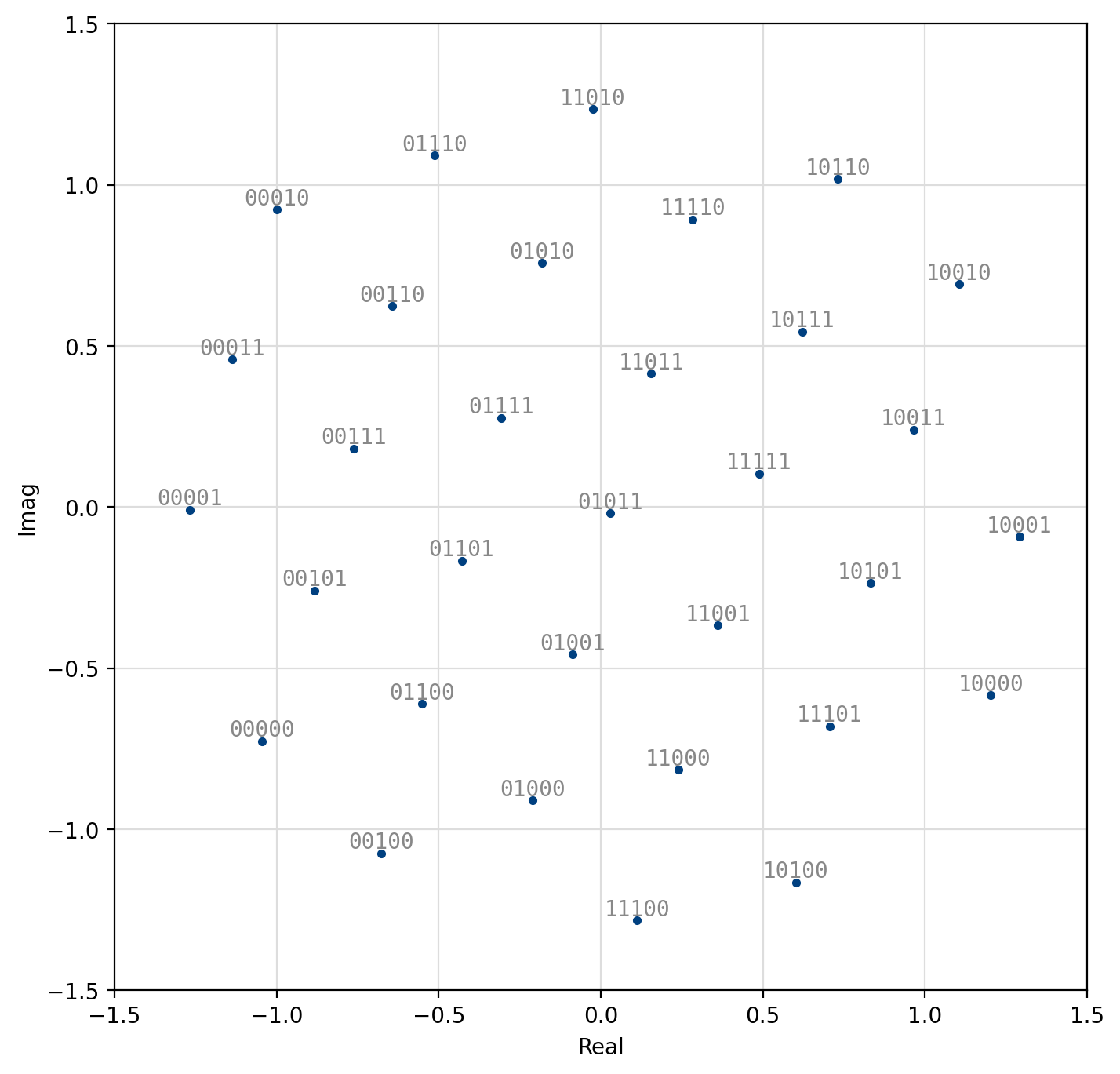
Figure 52 Optimal 32-QAM

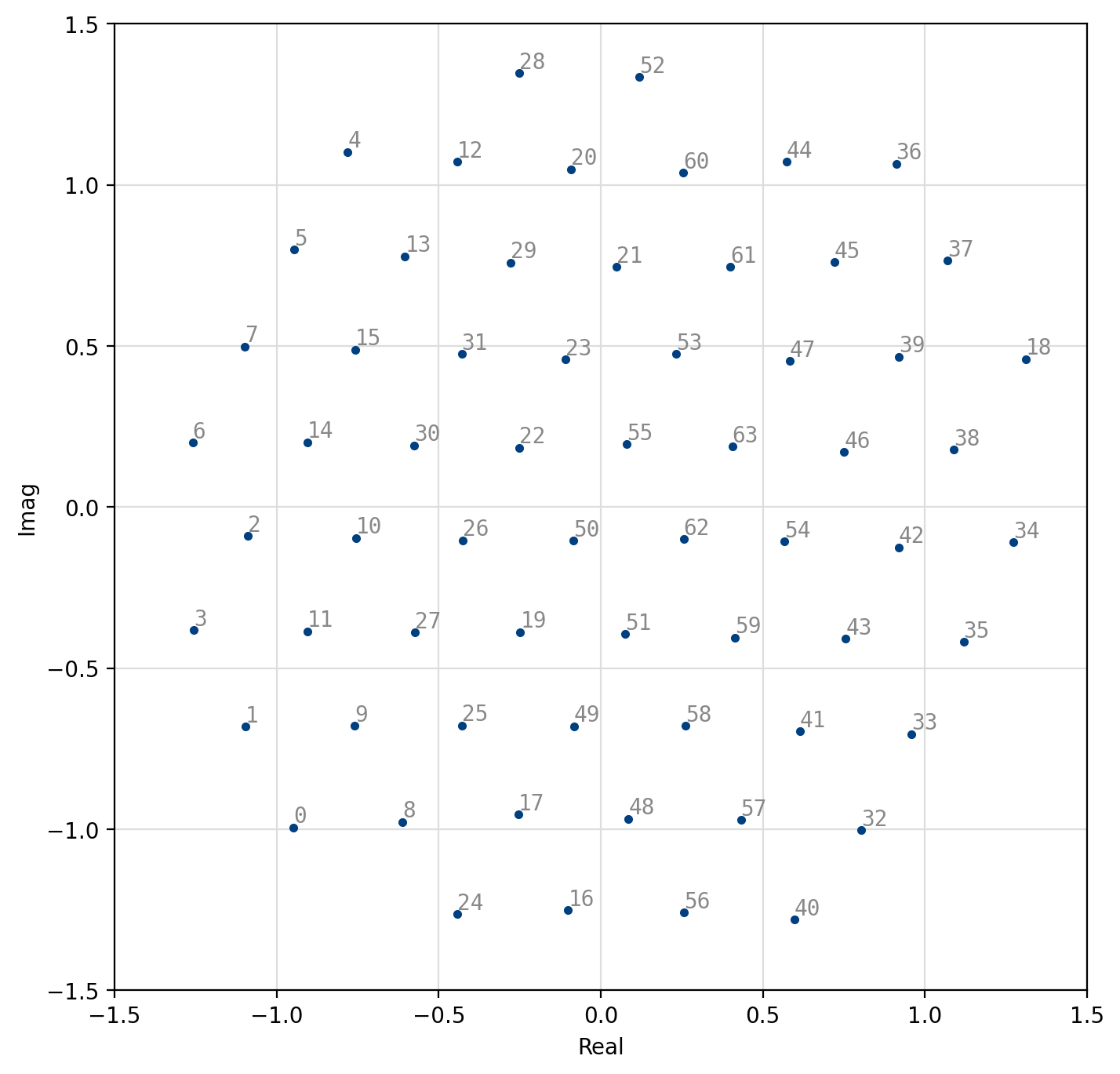
Figure 53 Optimal 64-QAM

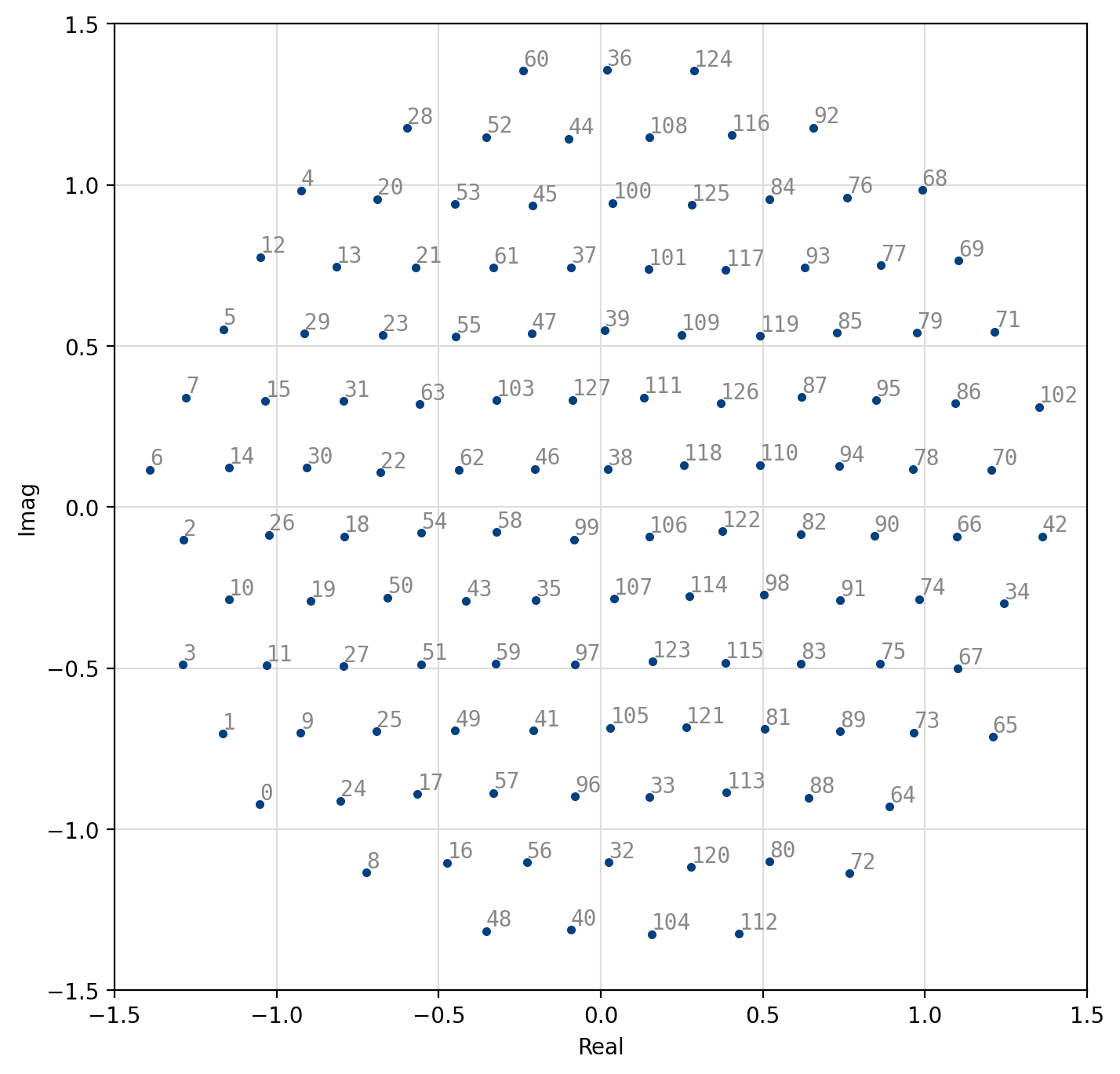
Figure 54 Optimal 128-QAM

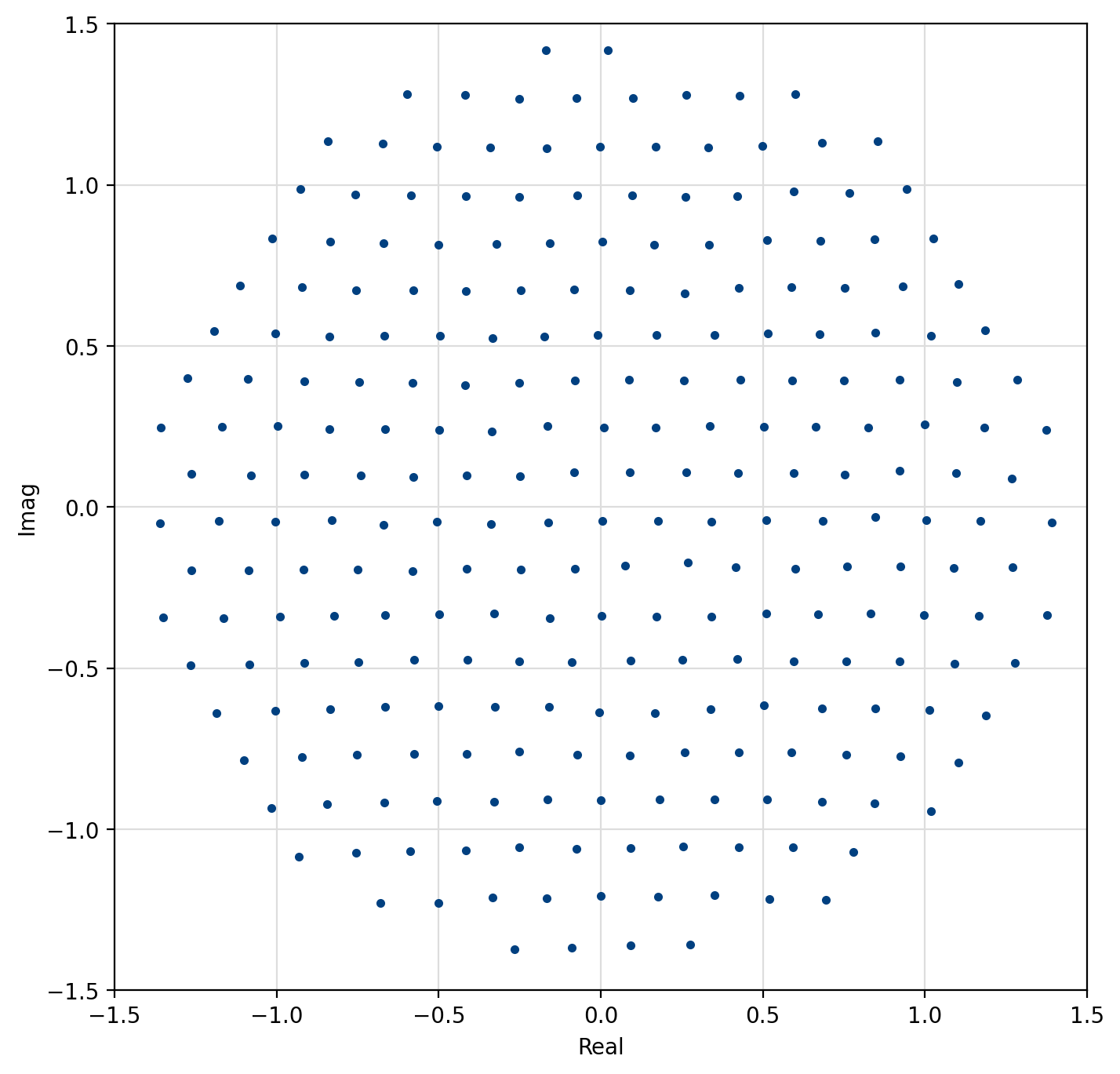
Figure 55 Optimal 256-QAM

[fig-modem-optqam] shows the constellation maps for the optimal QAM schemes. Notice that the constellations approximate a circle with each point falling on the lattice of equilateral triangles. Furthermore, adjacent constellation points differ by typically only a single bit to reduce the resulting bit error rate at the output of the demodulator. These constellations marginally out-perform regular square QAM (see Figures [fig-modem-M32] and [fig-modem-M128]) at the expense of a significantly increased computational complexity.

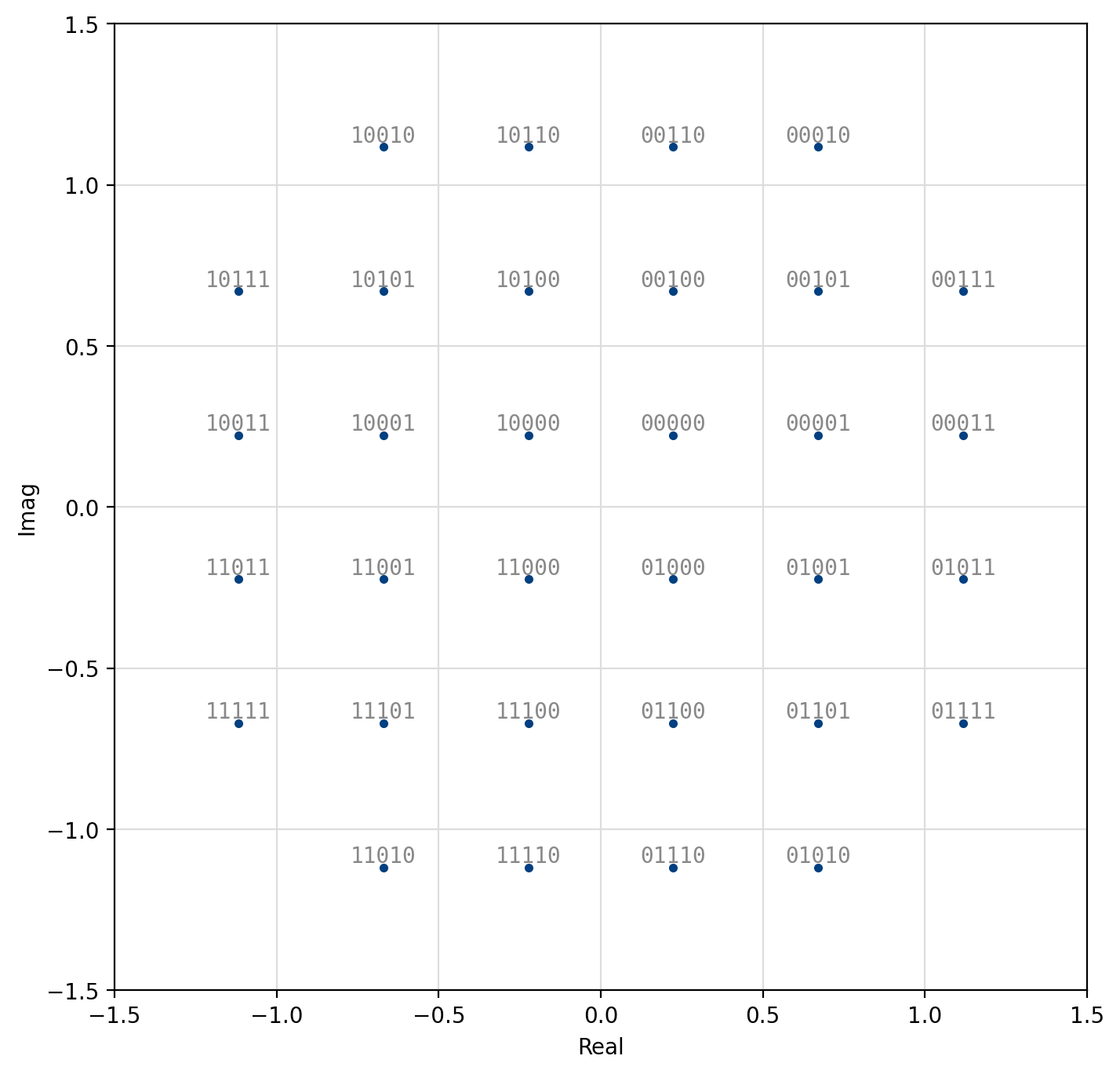
Figure 56 “Square” 32-QAM

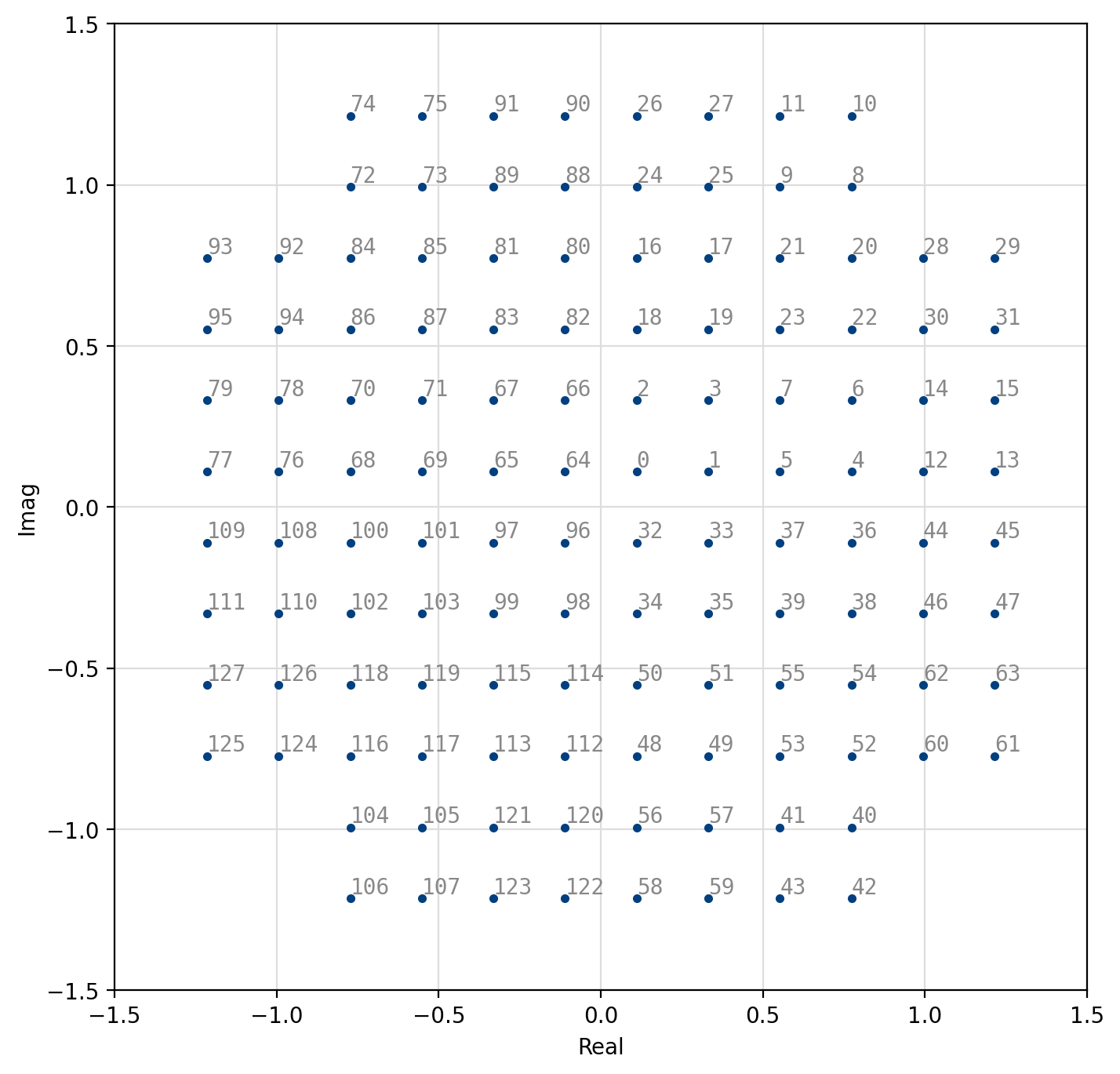
Figure 57 “Square” 128-QAM

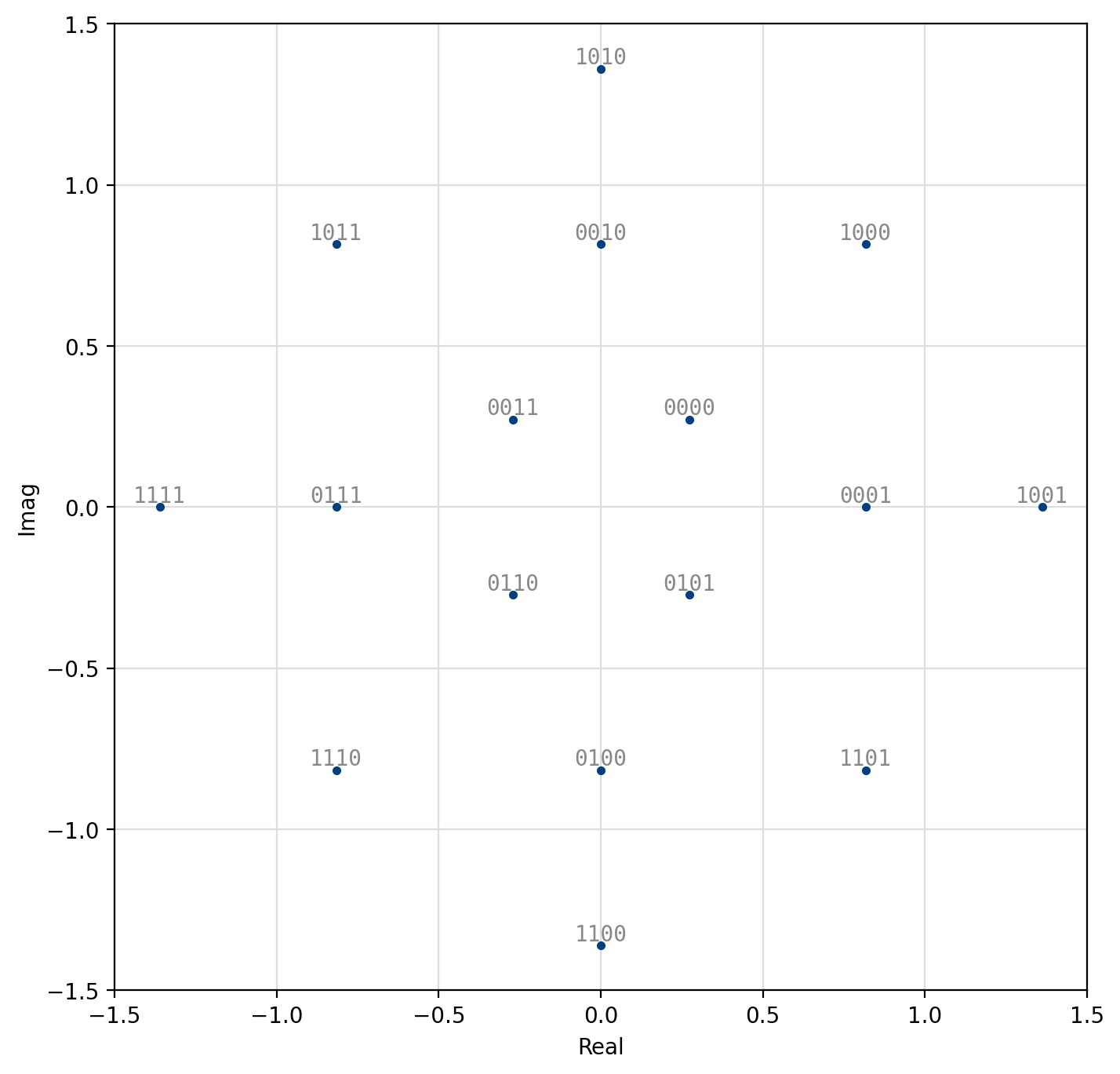
Figure 58 V.29

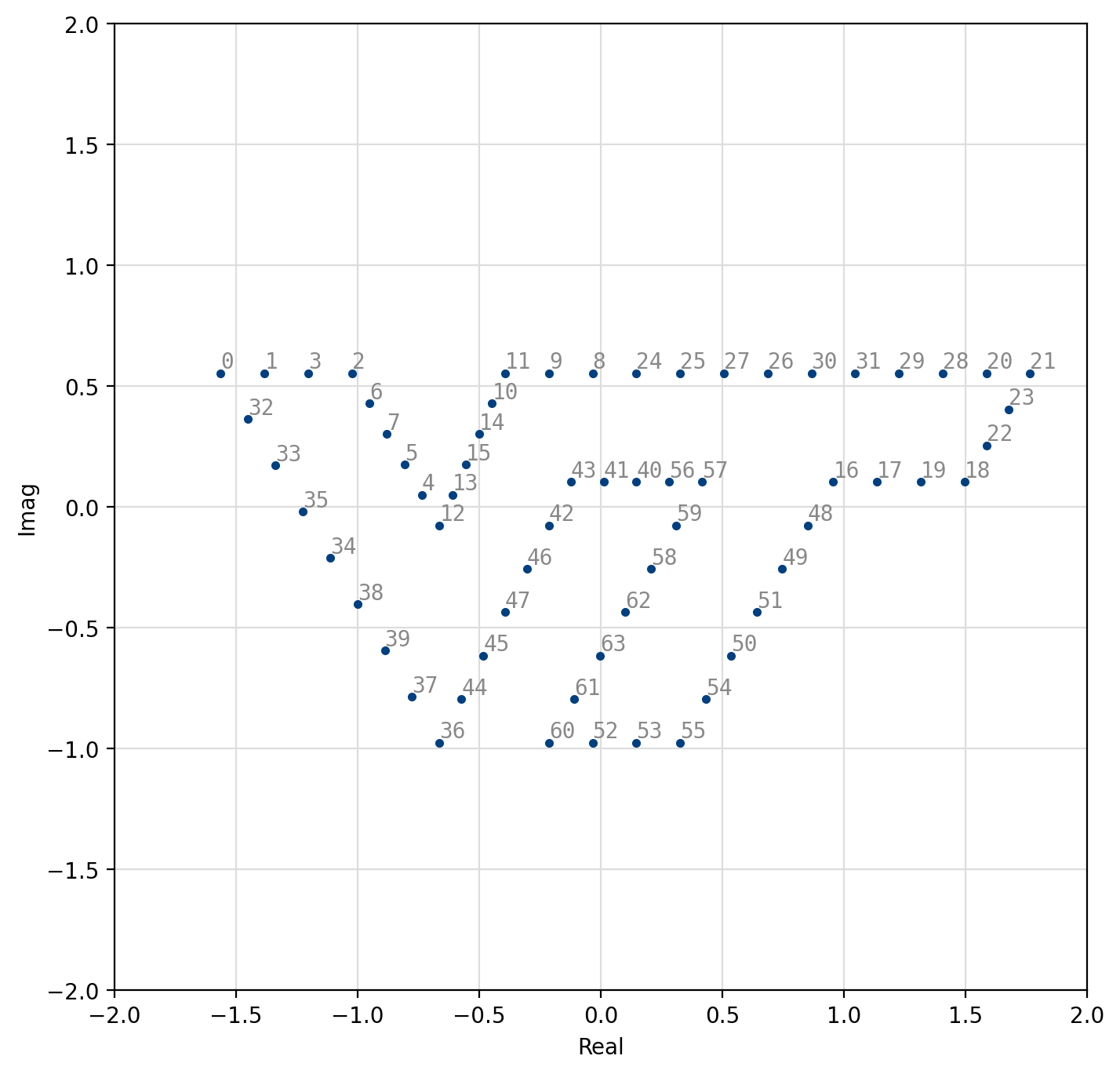
Figure 59 Arbitrary 64-QAM VT

[fig-modem-arb] depicts several available arbitrary constellation maps; however the user can create any arbitrary constellation map so long as no two points overlap (see modem_arb_init() and modem_arb_init_file() in [section-modem-digital-interface]).

Interface

While the same modem structure may be used for both modulation and demodulation for most schemes, it is important to use separate objects for differential-mode modems (e.g. LIQUID_MODEM_DPSK) as the internal state will change after each symbol. It is usually good practice to keep separate instances of modulators and demodulators. This holds true for most any encoder/decoder pair in liquid-dsp. An example of the modem interface is listed below.

Listed below is the full interface to the modem family of objects.

create()

Create digital modem object with a particular scheme

modemcf

modemcf = modemcf_create(modulation_scheme _scheme);

• modulation_scheme _scheme: linear modulation scheme (e.g. LIQUID_MODEM_QPSK)

• returns new modemcf object

modem

modem = modem_create(modulation_scheme _scheme);

• modulation_scheme _scheme: linear modulation scheme (e.g. LIQUID_MODEM_QPSK)

• returns new modem object

create_arbitrary()

Create linear digital modem object with arbitrary constellation points defined by an external table of symbols. Sample points are provided as complex float pairs and converted internally if needed.

modemcf

modemcf = modemcf_create_arbitrary(liquid_float_complex * _table, unsigned int _M);

• liquid_float_complex * _table: array of complex constellation points

• unsigned int _M: modulation order and table size

• returns new modemcf object

modem

modem = modem_create_arbitrary(liquid_float_complex * _table, unsigned int _M);

• liquid_float_complex * _table: array of complex constellation points

• unsigned int _M: modulation order and table size

• returns new modem object

recreate()

Recreate modulation scheme, re-allocating memory as necessary

modemcf

modemcf = modemcf_recreate(modemcf _q, modulation_scheme _scheme);

• modemcf _q: modem object

• modulation_scheme _scheme: linear modulation scheme (e.g. LIQUID_MODEM_QPSK)

• returns new modemcf object

modem

modem = modem_recreate(modem _q, modulation_scheme _scheme);

• modem _q: modem object

• modulation_scheme _scheme: linear modulation scheme (e.g. LIQUID_MODEM_QPSK)

• returns new modem object

copy()

Copy object including all internal objects and state

modemcf

modemcf = modemcf_copy(modemcf _q);

• modemcf _q:

• returns new modemcf object

modem

modem = modem_copy(modem _q);

• modem _q:

• returns new modem object

destroy()

Destroy modem object, freeing all allocated memory

modemcf

int = modemcf_destroy(modemcf _q);

• modemcf _q:

• returns standard error code

modem

int = modem_destroy(modem _q);

• modem _q:

• returns standard error code

print()

Print modem status to stdout

modemcf

int = modemcf_print(modemcf _q);

• modemcf _q:

• returns standard error code

modem

int = modem_print(modem _q);

• modem _q:

• returns standard error code

reset()

Reset internal state of modem object; note that this is only relevant for modulation types that retain an internal state such as LIQUID_MODEM_DPSK4 as most linear modulation types are stateless

modemcf

int = modemcf_reset(modemcf _q);

• modemcf _q:

• returns standard error code

modem

int = modem_reset(modem _q);

• modem _q:

• returns standard error code

gen_rand_sym()

Generate random symbol for modulation

modemcf

unsigned int = modemcf_gen_rand_sym(modemcf _q);

• modemcf _q:

• returns something good

modem

unsigned int = modem_gen_rand_sym(modem _q);

• modem _q:

• returns something good

get_bps()

Get number of bits per symbol (bps) of modem object

modemcf

unsigned int = modemcf_get_bps(modemcf _q);

• modemcf _q:

• returns something good

modem

unsigned int = modem_get_bps(modem _q);

• modem _q:

• returns something good

get_scheme()

Get modulation scheme of modem object

modemcf

modulation_scheme = modemcf_get_scheme(modemcf _q);

• modemcf _q:

• returns something good

modem

modulation_scheme = modem_get_scheme(modem _q);

• modem _q:

• returns something good

modulate()

Modulate input symbol (bits) and generate output complex sample

modemcf

int = modemcf_modulate(modemcf _q, unsigned int _s, float complex * _y);

• modemcf _q: modem object

• unsigned int _s: input symbol

• float complex * _y: output complex sample

• returns standard error code

modem

int = modem_modulate(modem _q, unsigned int _s, float complex * _y);

• modem _q: modem object

• unsigned int _s: input symbol

• float complex * _y: output complex sample

• returns standard error code

demodulate()

Demodulate input sample and provide maximum-likelihood estimate of symbol that would have generated it. The output is a hard decision value on the input sample. This is performed efficiently by taking advantage of symmetry on most modulation types. For example, square and rectangular quadrature amplitude modulation with gray coding can use a bisection search independently on its in-phase and quadrature channels. Arbitrary modulation schemes are relatively slow, however, for large modulation types as the demodulator must compute the distance between the received sample and all possible symbols to derive the optimal symbol.

modemcf

int = modemcf_demodulate(modemcf _q, float complex _x, unsigned int * _s);

• modemcf _q: modem object

• float complex _x: input sample

• unsigned int * _s: output hard symbol

• returns standard error code

modem

int = modem_demodulate(modem _q, float complex _x, unsigned int * _s);

• modem _q: modem object

• float complex _x: input sample

• unsigned int * _s: output hard symbol

• returns standard error code

demodulate_soft()

Demodulate input sample and provide (approximate) log-likelihood ratio (LLR, soft bits) as an output. Similarly to the hard-decision demodulation method, this is computed efficiently for most modulation types.

modemcf

int = modemcf_demodulate_soft(modemcf _q, float complex _x, unsigned int * _s, unsigned char * _soft_bits);

• modemcf _q: modem object

• float complex _x: input sample

• unsigned int * _s: output hard symbol

• unsigned char * _soft_bits: output soft bits

• returns standard error code

modem

int = modem_demodulate_soft(modem _q, float complex _x, unsigned int * _s, unsigned char * _soft_bits);

• modem _q: modem object

• float complex _x: input sample

• unsigned int * _s: output hard symbol

• unsigned char * _soft_bits: output soft bits

• returns standard error code

get_demodulator_sample()

Get demodulator’s estimated transmit sample

modemcf

int = modemcf_get_demodulator_sample(modemcf _q, float complex * _x_hat);

• modemcf _q:

• float complex * _x_hat:

• returns standard error code

modem

int = modem_get_demodulator_sample(modem _q, float complex * _x_hat);

• modem _q:

• float complex * _x_hat:

• returns standard error code

get_demodulator_phase_error()

Get demodulator phase error

modemcf

float = modemcf_get_demodulator_phase_error(modemcf _q);

• modemcf _q:

• returns something good

modem

float = modem_get_demodulator_phase_error(modem _q);

• modem _q:

• returns something good

get_demodulator_evm()

Get demodulator error vector magnitude

modemcf

float = modemcf_get_demodulator_evm(modemcf _q);

• modemcf _q:

• returns something good

modem

float = modem_get_demodulator_evm(modem _q);

• modem _q:

• returns something good