Nakagami-\(m\)

The Nakagami-\(m\) distribution is a versatile stochastic model for modeling radio links [BD91] and has often been regarded as the best distribution to model land mobile propagation due to its ability to describe fading situations worse than Rayleigh, including one-sided Gaussian [SA98]. Empirical evidence regarding the efficacy the Nakagami-\(m\) distribution has on fading profiles been presented in [Suz77, Tur80]. Thus statistical inference of the Nakagami-\(m\) fading parameters are of interest in the design of adaptive radios such as optimized transmit diversity modes [Cav99, KA03] and adaptive modulation schemes [CEH02]. The Nakagami-\(m\) probability density function is given by [PP02]

(46)\[\begin{split}f_X(x;m,\Omega) = \begin{cases} \frac{2}{\Gamma(m)} \left( \frac{m}{\Omega} \right)^m x^{2m-1} e^{ -(m/\Omega)x^2} & x \ge 0 \\ 0 & \text{else}. \end{cases}\end{split}\]

where \(m \ge 1/2\) is the shape parameter and \(\Omega \gt 0\) is the spread parameter. Nakagami-\(m\) random numbers are generated from the gamma distribution. Specifically if \(R\) follows a gamma distribution defined by (45) with parameters \(\alpha\) and \(\beta\), then \(X=\sqrt{R}\) has a Nakagami-\(m\) distribution with \(m=\alpha\) and \(\Omega=\beta/\alpha\).

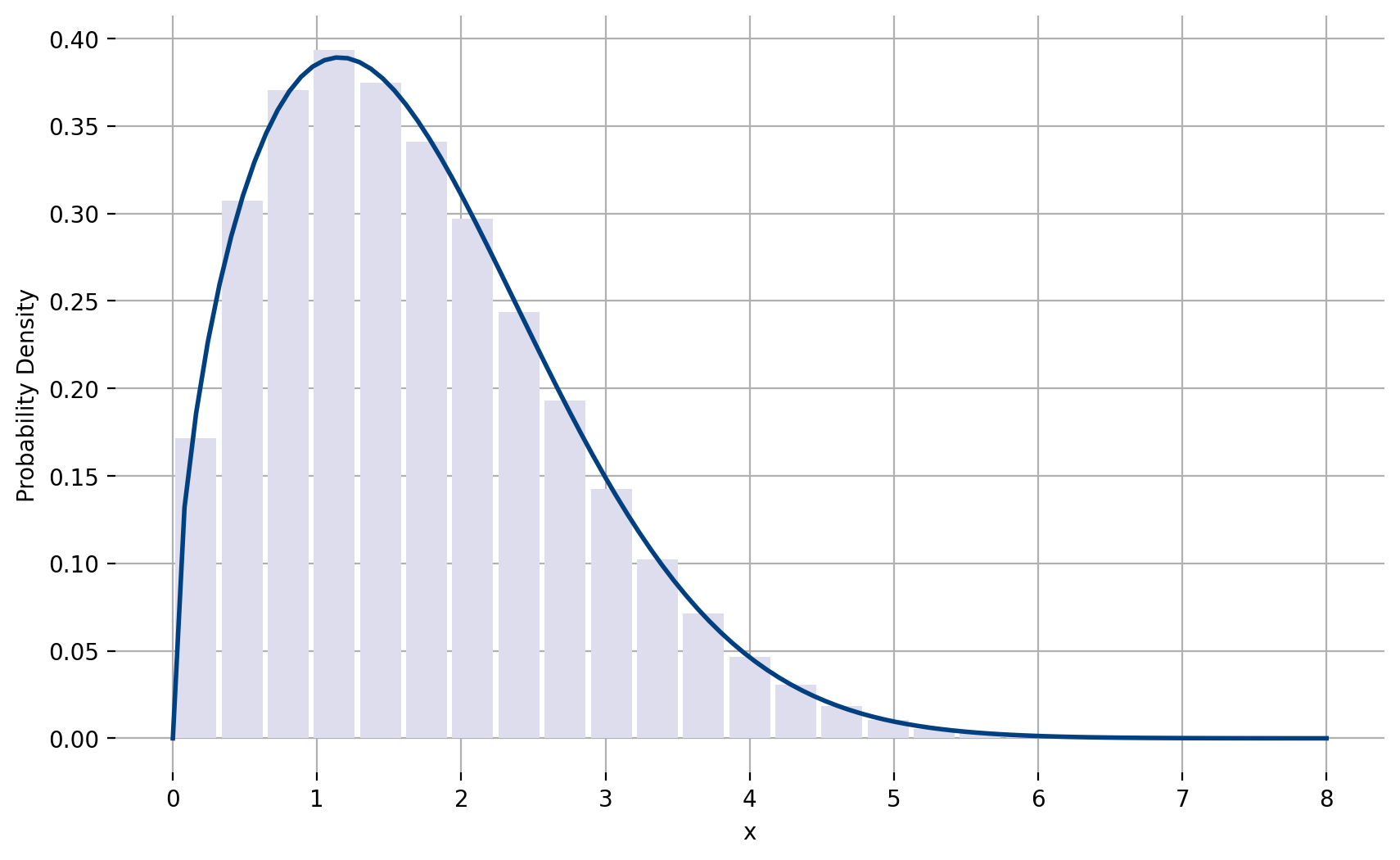
Figure 62 Nakagami-\(m\) distribution with \(m=0.75\) and \(\Omega=4\)

Interface

Nakagami random number generator interface:

// generate a Nakagami-m random variable
float randnakmf(float _m,
                float _omega);

// compute a Nakagami-m probability density
float randnakmf_pdf(float _x,
                    float _m,
                    float _omega);

// compute a Nakagami-m cumulative distribution
float randnakmf_cdf(float _x,
                    float _m,
                    float _omega);