Butterworth IIR Filter Design

LIQUID_IIRDES_BUTTER is a Butterworth filter. This is an all-pole analog design that has a maximally flat magnitude response in the pass-band. The analog prototype interface is butter_azpkf() which computes the \(n\) complex roots \(p_{a0},p_{a1},\ldots,p_{an-1}\) of the \(n^{th}\)-order Butterworth polynomial,

(31)\[p_{ak} = \omega_c \exp\left\{ j \frac{\left(2k+n+1\right)\pi}{2n} \right\}\]

for \(k=0,1,\ldots,n-1\). Note that this results in a set of complex conjugate pairs such that \((-1)^n s_0 s_1 \cdots s_{n-1} = 1\).

An example Butterworth design can be seen in the code listing here:

#include <liquid/liquid.h>
int main()
{
    return 0;
}

An example of a digital Butterworth filter response can be found in the figure, below for an order 3:

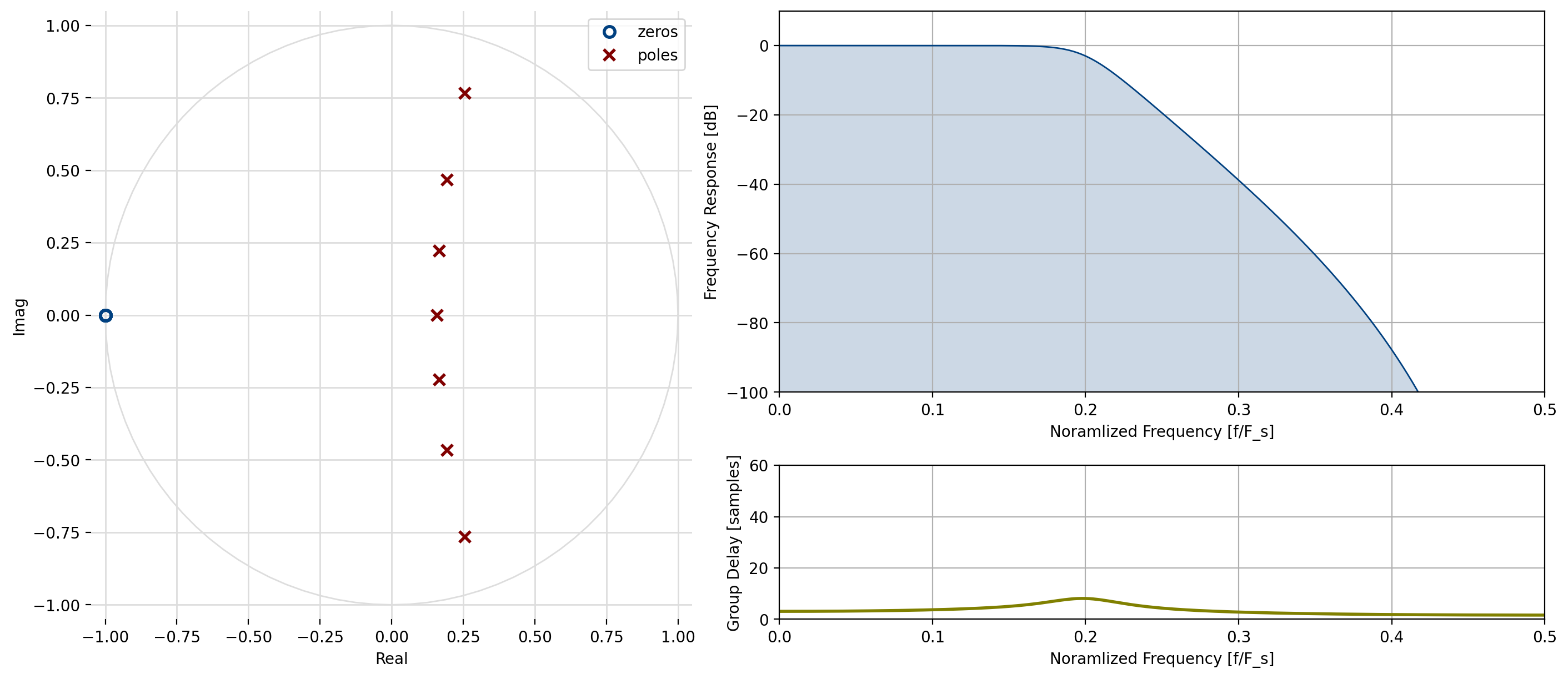
Figure 12 Butterworth filter design, \(n=7\), \(f_c=0.2 F_s\)

Notice how the performance changes as the order increases to 15:

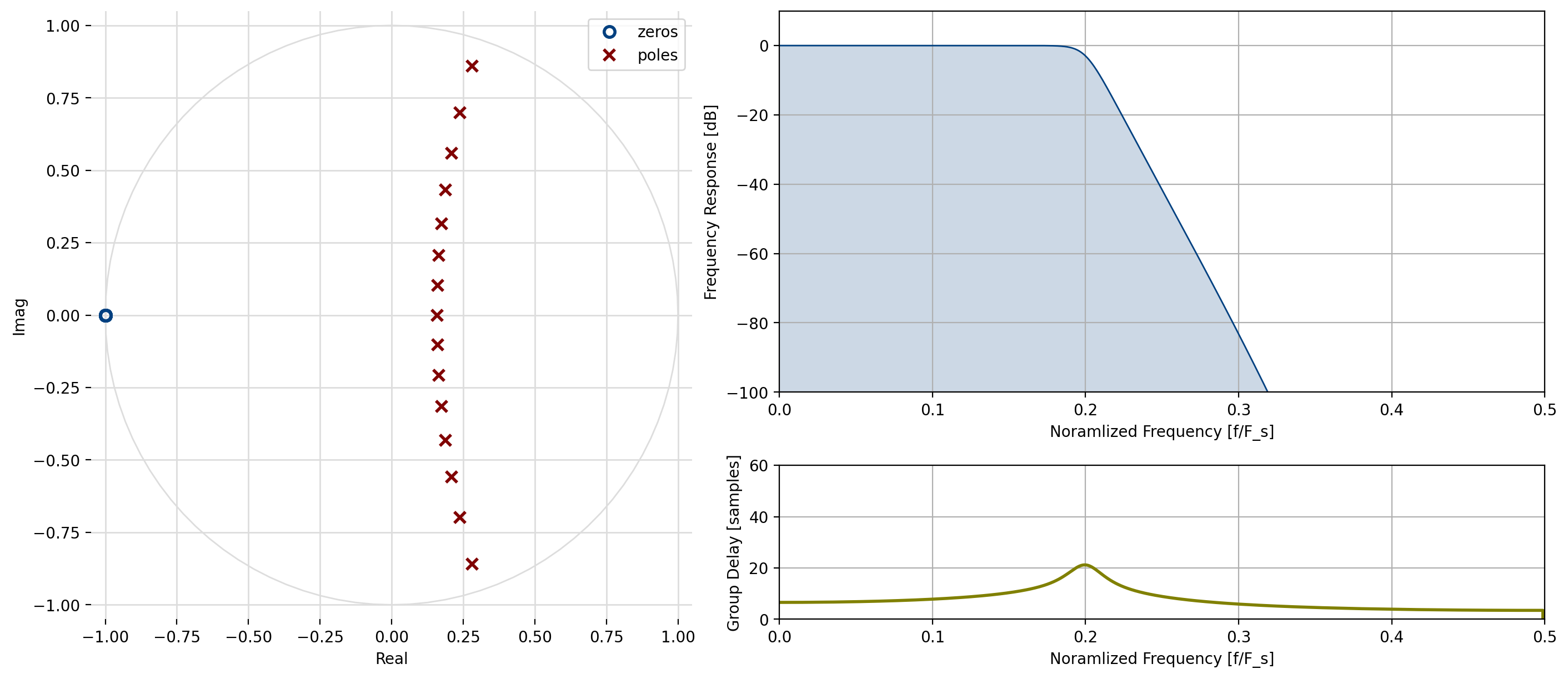
Figure 13 Butterworth filter design, \(n=15\), \(f_c=0.1 F_s\)

Notice how the poles change when the cutoff frequency drops to \(0.1 F_s\):

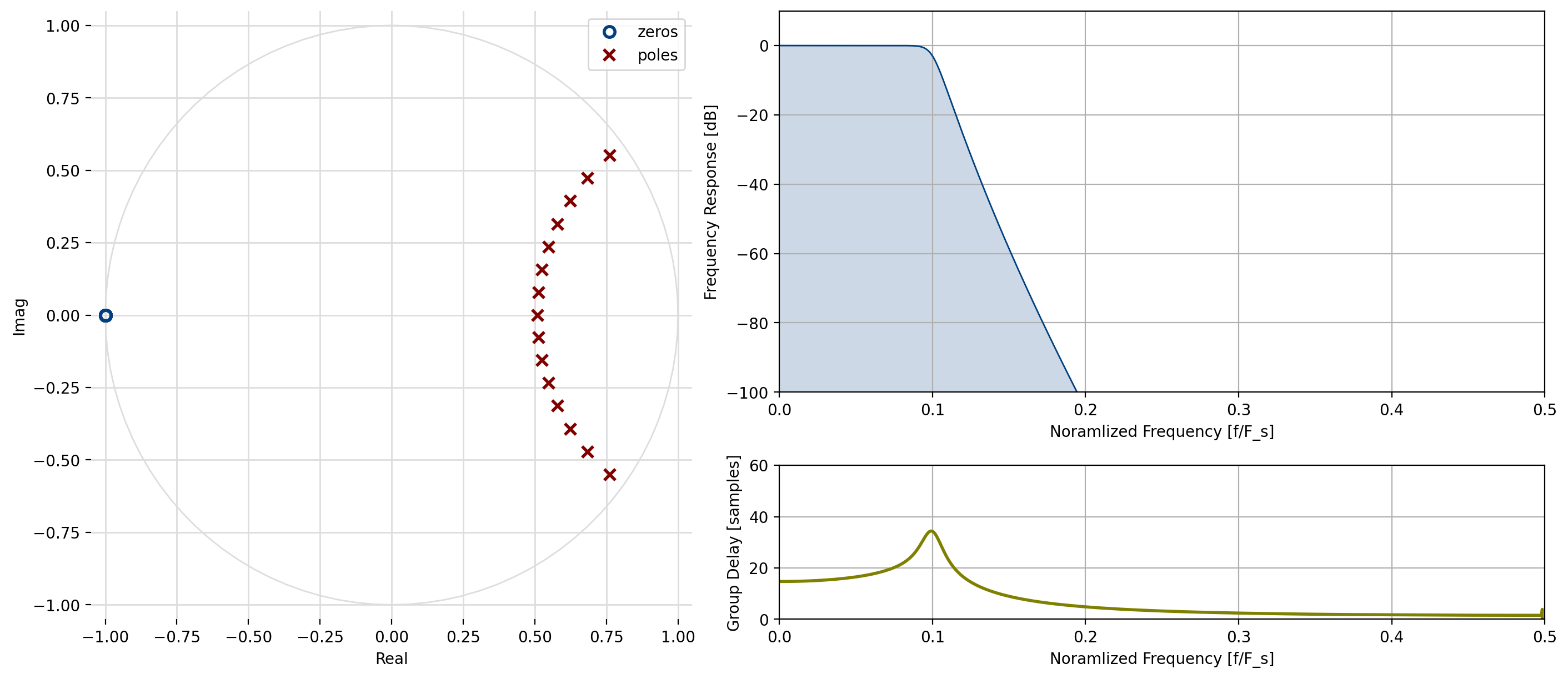
Figure 14 Butterworth filter design, \(n=15\), \(f_c=0.1 F_s\)